题目内容
7.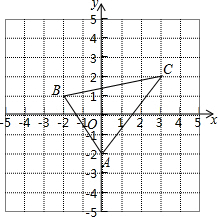 如图、已知A(0、-2)、B(-2、1)、C(3、2)
如图、已知A(0、-2)、B(-2、1)、C(3、2)(1)求线段AB、AC的长.
(2)把A、B、C 三点的横坐标、纵坐标都乘以2得到A1、B1、C1的坐标.求A1B1、A1C1的长.
(3)以上四条线段成比例吗?说明理由.
分析 (1)根据勾股定理即可求得AB、AC的长度;
(2)根据A、B、C三点新的坐标即可根据勾股定理求A1B1、A1C1的长;
(3)由(1)和(2)中的数据计算比值验证即可.
解答 解:(1)∵A(0、-2)、B(-2、1)、C(3、2),
∴由勾股定理得:AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
AC=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)由已知得A1(0,-4),B1(-4,2),C2(6,4),
由勾股定理得:A1B1=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
A1C1=$\sqrt{{6}^{2}+{8}^{2}}$=10;
(3)以上四条线段成比例,理由如下:
∵$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{\sqrt{13}}{2\sqrt{13}}$=$\frac{1}{2}$,$\frac{AC}{{A}_{1}{C}_{1}}$=$\frac{5}{10}$=$\frac{1}{2}$,
∴$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{AC}{{A}_{1}{C}_{1}}$,
∴四条线段成比例.
点评 本题考查了比例线段:对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如ab=cd(即ad=bc),我们就说这四条线段是成比例线段,简称比例线段.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列各式计算正确的是( )
| A. | a•a2=a2 | B. | a5-a3=a2 | C. | (-a)3=-a3 | D. | (ab)2=ab2 |
2.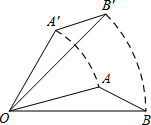 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是( )
 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是( )| A. | 21° | B. | 45° | C. | 42° | D. | 24° |
19.若点A(x1,y1),B(x2,y2)在反比例函数y=$\frac{k-3}{x}$(x>0)图象上,当x1<x2时,y1<y2,则k的取值范围是( )
| A. | k<3 | B. | k≤3 | C. | k>3 | D. | k≥3 |
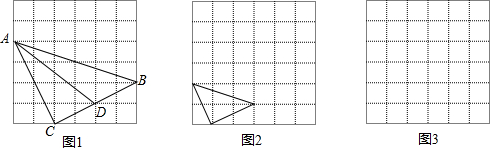
 如图,在Rt△ABC中,CD是斜边AB的中线,MN是中位线,试证明CD=MN.
如图,在Rt△ABC中,CD是斜边AB的中线,MN是中位线,试证明CD=MN.