题目内容
16.定义:有三个角相等的四边形叫做三等角四边形.(1)在三等角四边形ABCD中,∠A=∠B=C,则∠A的取值范围为60°<∠BAD<120°.
(2)如图①,折叠平行四边形DEBF,使得顶点E、F分别落在边BE、BF上的点A、C处,折痕为DG、DH.
求证:四边形ABCD为三等角四边形;
(3)如图②,三等角四边形ABCD中,∠A=∠B=∠C,若AB=5,AD=$\sqrt{26}$,DC=7,则BC的长度为$\frac{6}{13}$$\sqrt{26}$.

分析 (1)根据四边形的内角和是360°,确定出∠BAD的范围;
(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC即可;
(3)延长BA,过D点作DG⊥BA,继续延长BA,使得AG=EG,连接DE;延长BC,过D点作DH⊥BC,继续延长BC,使得CH=HF,连接DF,由SAS证明△DEG≌△DAG,得出AD=DE=$\sqrt{26}$,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=7,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=7,DE=BF=$\sqrt{26}$,由等腰三角形的性质得出EG=AG=$\frac{1}{2}$(BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=$\sqrt{A{D}^{2}-A{G}^{2}}$=5,由平行四边形DEBF的面积求出DH=$\frac{35}{26}$$\sqrt{26}$,在Rt△DCH中,由勾股定理求出CH=$\frac{7}{26}$$\sqrt{26}$,即可得出BC的长度.
解答 (1)解:∵∠BAD=∠B=∠BCD,
∴3∠BAD+∠ADC=360°,
∴∠ADC=360°-3∠BAD.
∵0<∠ADC<180°,
∴0°<360°-3∠BAD<180°,
∴60°<∠BAD<120°;
故答案为:60°<∠BAD<120°;
(2)证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,DE∥BF,
∴∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,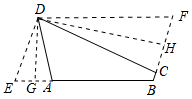
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形;
(3)解:延长BA,过D点作DG⊥BA,继续延长BA,使得AG=EG,连接DE;延长BC,过D点作DH⊥BC,继续延长BC,使得CH=HF,连接DF,如图所示:
在△DEG和△DAG中,$\left\{\begin{array}{l}{AG=EG}\\{∠AGD=∠EGD=90°}\\{DG=DG}\end{array}\right.$,
∴△DEG≌△DAG(SAS),
∴AD=DE=$\sqrt{26}$,∠DAG=∠DEA,
在△DFH和△DCH中,$\left\{\begin{array}{l}{CH=HF}\\{∠DHC=∠DHF=90°}\\{DH=DH}\end{array}\right.$,
∴△DFH≌△DCH(SAS),
∴CD=DF=7,∠DCH=∠DFH,
∵∠BAD=∠B=∠BCD,
∴∠DEB+∠B=180°,∠DFB+∠B=180°,
∴DE∥BF,BE∥DF,
∴四边形DEBF是平行四边形,
∴DF=BE=7,DE=BF=$\sqrt{26}$,
∴EG=AG=$\frac{1}{2}$(BE-AB)=$\frac{1}{2}$×(7-5)=1,
在Rt△DGA中,DG=$\sqrt{A{D}^{2}-A{G}^{2}}$=$\sqrt{(\sqrt{26})^{2}-{1}^{2}}$=5,
∵平行四边形DEBF的面积=BE•DG=DH•BF,
即:7×5=DH×$\sqrt{26}$,
∴DH=$\frac{35}{26}$$\sqrt{26}$,
在Rt△DCH中,CH=$\sqrt{D{C}^{2}-D{H}^{2}}$=$\sqrt{(7)^{2}-({\frac{35}{26}\sqrt{26})}^{2}}$=$\frac{7}{26}$$\sqrt{26}$,
∴BC=BF-2CH=$\sqrt{26}$-2×$\frac{7}{26}$$\sqrt{26}$=$\frac{6}{13}$$\sqrt{26}$;
故答案为:$\frac{6}{13}$$\sqrt{26}$.
点评 本题是四边形综合题目,考查了三等角四边形的判定与性质,翻折变换-折叠问题,四边形的内角和定理,平行四边形的判定与性质,全等三角形的判定与性质,正方形的性质,勾股定理,等腰三角形的性质等知识;本题综合性强,有一定难度,证明三角形全等和运用勾股定理是解决问题的关键.

 为了解今年全县2000名初二学生“创新能力大赛”的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据提供的信息,解答下列问题:
为了解今年全县2000名初二学生“创新能力大赛”的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据提供的信息,解答下列问题:(1)此次调查的样本容量为400.
(2)在表中:m=160;n=0.3;h=0.4.
(3)补全频数分布直方图;
(4)根据频数分布表、频数分布直方图,你获得哪些信息?
| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.1 |
| 70≤x≤80 | 120 | n |
| 80≤x<90 | m | h |
| 90≤x<100 | 80 | 0.2 |
| 自动铅笔(单位:支) | 笔记本(单位:本) | 总销售额(元) | |
| A | 20 | 32 | 72 |
| B | 10 | 36 | 56 |
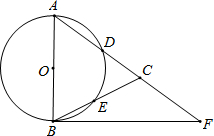 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB. 如图,点A、B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
如图,点A、B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.