题目内容
8.计算:$\sqrt{12}$-|-$\sqrt{3}$|+(-$\frac{1}{2}$)-2-sin60°.分析 原式第一项化为最简二次根式,第二项利用绝对值的代数意义化简,第三项利用负整数指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果.
解答 解:原式=2$\sqrt{3}$-$\sqrt{3}$+4-$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$+4.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
19.下列不等式变形正确的是( )
| A. | 由4x-1≥0得4x>1 | B. | 由5x>3 得 x>3 | C. | 由$\frac{y}{2}$>0得 y>0 | D. | 由-2x<4得x<-2 |
20.在平面直角坐标系中,点(m-2,m-3)在第三象限,则m的取值范围是( )
| A. | m>3 | B. | m<2 | C. | 2<m<3 | D. | m<3 |
17.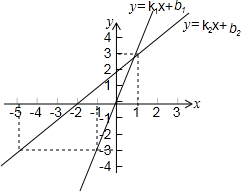 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )| A. | x<-1 | B. | -5<x<1 | C. | -5<x<-1 | D. | -1<x<1 |
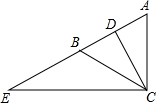 如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD=$\frac{1}{2}$CE.
如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB到点E,使BE=AB,连接CE.求证:CD=$\frac{1}{2}$CE.