题目内容
5.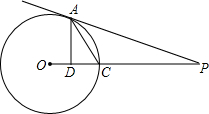 如图,PA是⊙O的切线,A为切点,PO交⊙O于D,AD⊥PO于点D,求证:∠PAC=∠CAD.
如图,PA是⊙O的切线,A为切点,PO交⊙O于D,AD⊥PO于点D,求证:∠PAC=∠CAD.
分析 遇切线,想直角.根据切线的性质,证明∠OAC+∠CAP=90°,根据AD⊥OC,证得∠OCA+∠DAC=90°,根据圆的半径都相等,易证∠OAC=∠OCA,根据相等角的余角相等,即可证得结论.
解答 解:如右图,连接OA,
∵PA是⊙O的切线,
∴∠OAP=90°,
即∠3+∠2+∠1=90°,
∵AD⊥PO,
∴∠ADC=90°,
∴∠2+∠4=90°,
∵OA=OC,
∴∠3+∠2=∠4,
∴∠1=∠2,
即∠PAC=∠CAD.
点评 本题主要考查了切线的性质、直角三角形的性质、等腰三角形的性质的综合应用,遇到切线,想到直角是解决此类问题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
16.下列说法错误的是( )
| A. | 经过平移,对应点所连的线段平行且相等 | |
| B. | 经过平移,对应线段平行 | |
| C. | 平移中,图形上每个点移动的距离可以不同 | |
| D. | 平移不改变图形的形状和大小 |
