题目内容
7.在平面直角坐标系中中,O为坐标原点,点A的坐标为(a,-a),点B的坐标为(b,c),且a,b,c满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{2a-4b-2c=-8}\end{array}\right.$(1)求证:a=b;
(2)若点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,求点B的坐标.
分析 (1)解方程组$\left\{\begin{array}{l}{3a-b+2c=8}\\{2a-4b-2c=-8}\end{array}\right.$即可得到结论;
(2)利用A(a,-a)和B(a,4-a)得到AB=4,AB与y轴平行,由于点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,则判断点A、点B在y轴的右侧,即a>0,根据三角形面积公式得到$\frac{1}{2}$×4×a=2×$\frac{1}{2}$×4×|4-a|,解方程得a=$\frac{8}{3}$或a=8,然后写出B点坐标.
解答 解:(1)解方程组$\left\{\begin{array}{l}{3a-b+2c=8}\\{2a-4b-2c=-8}\end{array}\right.$,得b=a;
(2)解方程组$\left\{\begin{array}{l}{3a-b+2c=8}\\{2a-4b-2c=-8}\end{array}\right.$得b=a,c=4-a,
∵点A的坐标为(a,-a),点B坐标为(b,c),
∴B点坐标为(a,4-a),
∴AB=4,AB与y轴平行,
∵点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,
∴点A、点B在y轴的右侧,即a>0,
∴$\frac{1}{2}$×4×a=2×$\frac{1}{2}$×4×|4-a|,解得a=$\frac{8}{3}$或a=8,
∴B点坐标为($\frac{8}{3}$,$\frac{4}{3}$)或(8,-4).
点评 本题考查了坐标与图形性质:利用点的坐标计算线段的长和判断线段与坐标轴的位置关系.也考查了三角形的面积公式.

练习册系列答案
相关题目
4.体育课上,全班男同学进行了100米测验,达标成绩为15秒,下表是某小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
问:(1)这个小组男生的达标率为多少?
(2)这个小组男生的平均成绩是多少秒?
| -0.87 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
(2)这个小组男生的平均成绩是多少秒?
2.已知在线段上依次添加1点,2点,3点,…,原线段上所成线段的总条数如表.
若在原线段上添加n个点,则原线段上所有线段总条数为( )
| 图形 |  |  |  |  |
| 线段总条数 | 3 | 6 | 10 | 15 |
| A. | n+2 | B. | 1+2+3+…+n+n+1 | C. | n+1 | D. | $\frac{n(n+1)}{2}$ |
12.计算(-2x2y)2的结果是( )
| A. | -2x4y2 | B. | 4x4y2 | C. | -4x2y | D. | 4x4y |
19.某服装原价200元,连续两次涨价,每次都涨a%后的价格为242元,则a是( )
| A. | 20 | B. | 15 | C. | 10 | D. | 5 |
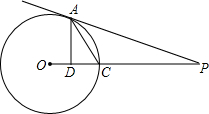 如图,PA是⊙O的切线,A为切点,PO交⊙O于D,AD⊥PO于点D,求证:∠PAC=∠CAD.
如图,PA是⊙O的切线,A为切点,PO交⊙O于D,AD⊥PO于点D,求证:∠PAC=∠CAD.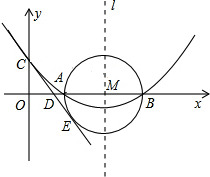 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边). 求证:全等三角形对应边上的高线相等.
求证:全等三角形对应边上的高线相等.