题目内容
已知方程-x2+x+m=0有两个不相等的实根,则抛物线y=-x2+x+m的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:抛物线与x轴的交点
专题:
分析:易证抛物线与x轴有2个交点,根据抛物线开口向下,即可求得抛物线顶点在第一或者第二象限,再根据对称轴在y轴右侧,即可解题.
解答:解:∵方程-x2+x+m=0有两个不相等的实根,
∴抛物线y=-x2+x+m与x轴有2个交点,
∵抛物线y=-x2+x+m开口向下,
∴抛物线顶点在第一或者第二象限,
∵抛物线y=-x2+x+m对称轴为y=-
=
>0,
∴抛物线y=-x2+x+m顶点在第一象限,
故选:A.
∴抛物线y=-x2+x+m与x轴有2个交点,
∵抛物线y=-x2+x+m开口向下,
∴抛物线顶点在第一或者第二象限,
∵抛物线y=-x2+x+m对称轴为y=-
| b |
| 2a |
| 1 |
| 2 |
∴抛物线y=-x2+x+m顶点在第一象限,
故选:A.
点评:本题考查了抛物线开口方向的求解,考查了抛物线对称轴的求解,本题中求抛物线开口和对称轴是解题的关键.

练习册系列答案
相关题目
若关于x的方程
-
=0有增根,则a的值是( )
| a-3 |
| x-3 |
| x |
| x-3 |
| A、3 | B、6 | C、-6 | D、-3 |

 如图所示的是由小正方体搭成的几何体的俯视图.小正方形中的数字表示该位置的小正方体的个数,请画出该几何体的主视图和左视图.
如图所示的是由小正方体搭成的几何体的俯视图.小正方形中的数字表示该位置的小正方体的个数,请画出该几何体的主视图和左视图.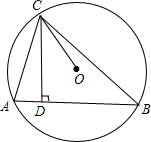 如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.
如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO. 如图,已知∠α.
如图,已知∠α.