题目内容
已知轮船在静水中的速度是32km/h,水流的速度是4km/h,那么该轮船顺流航行的速度是 ,逆流航行的速度是 ,若这艘轮船在甲乙两码头间往返一次共用4h,则甲乙两码头之间的距离是 .
考点:一元一次方程的应用
专题:
分析:根据顺流速度=静水速度+水流速度,求出该轮船顺流航行的速度;由逆流速度=静水速度-水流速度,求出逆流航行的速度;设甲乙两码头之间的距离是xkm,根据“这艘轮船在甲乙两码头间往返一次共用4h”列出方程,解方程即可.
解答:解:∵轮船在静水中的速度是32km/h,水流的速度是4km/h,
∴该轮船顺流航行的速度是32+4=36(km/h),逆流航行的速度是32-4=28(km/h).
设甲乙两码头之间的距离是xkm,根据题意得
+
=4,
解得x=63.
即甲乙两码头之间的距离是63km.
故答案为36km/h,28km/h,63km.
∴该轮船顺流航行的速度是32+4=36(km/h),逆流航行的速度是32-4=28(km/h).
设甲乙两码头之间的距离是xkm,根据题意得
| x |
| 36 |
| x |
| 28 |
解得x=63.
即甲乙两码头之间的距离是63km.
故答案为36km/h,28km/h,63km.
点评:此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程求解.顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
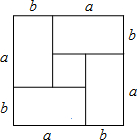 如图分割正方形,可以验证( )
如图分割正方形,可以验证( )| A、(a+b)2=a2-2ab+b2 |
| B、(a-b)2=a2-2ab+b2 |
| C、(a+b)2=(a-b)2+4ab |
| D、(a+b)(a-b)=a2-b2 |
已知方程-x2+x+m=0有两个不相等的实根,则抛物线y=-x2+x+m的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
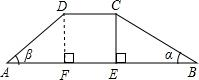 如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1,坝顶宽DC=2.5m,坝高5m.(整个大坝长5km,不改变坡角与坝底),需要多少土方?
如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1,坝顶宽DC=2.5m,坝高5m.(整个大坝长5km,不改变坡角与坝底),需要多少土方?