题目内容
6.解方程组:$\left\{\begin{array}{l}{|x+3|+|y-2|=9}\\{|x+3|-2y+4=0}\end{array}\right.$.分析 先利用加减消元法消去x得到|y-2|+2y-4=9,则进行分类讨论:当y≤2时,-y+2+2y-4=9,解得y=11(舍去),当y>2时,y-2+2y-4=9,解得y=5,然后利用代入法求出x即可得到方程组的解.
解答 解:$\left\{\begin{array}{l}{|x+3|+|y-2|=9①}\\{|x+3|-2y+4=0②}\end{array}\right.$
①-②得|y-2|+2y-4=9,
当y≤2时,-y+2+2y-4=9,
解得y=11(舍去),
当y>2时,y-2+2y-4=9,
解得y=5,
把y=5代入①得|x+3|+3=9,
解得x=3或x=-9.
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=-9}\\{y=5}\end{array}\right.$.
点评 本题考查了解二元一次方程组:利用代入消元法或加减消元法解二元一次方程组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
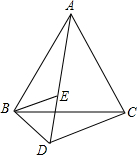 如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度?
如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度?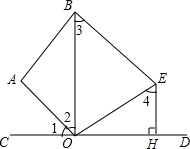 如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.
如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.