题目内容
已知:△ABC,△DEF都是等边三角形,M是BC与EF的中点,连接AD,BE.
(1)如图1,当EF与BC在同一条直线上时,直接写出AD与BE的数量关系和位置关系;
(2)△ABC固定不动,将图1中的△DEF绕点M顺时针旋转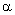 (
(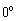 ≤
≤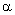 ≤
≤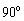 )角,如图2所示,判断(1)中的结论是否仍然成立,若成立,请加以证明;若不成立,
)角,如图2所示,判断(1)中的结论是否仍然成立,若成立,请加以证明;若不成立, 说明理由;
说明理由;
(3)△ABC固定不动,将图1中的△DEF绕点M旋转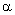 (
(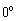 ≤
≤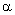 ≤
≤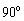 )角,作DH⊥B
)角,作DH⊥B C于点H.设BH=x,线段AB,BE,ED,DA所围成的图形面积为S.当A
C于点H.设BH=x,线段AB,BE,ED,DA所围成的图形面积为S.当A B=6,DE=2时,求S关于x的函数关系式,并写出相应的x的取值范围.
B=6,DE=2时,求S关于x的函数关系式,并写出相应的x的取值范围.
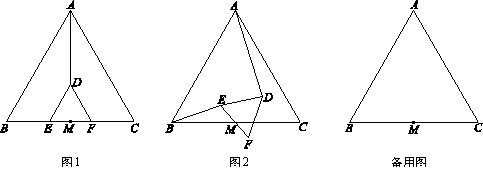 |
(1) ,
, .
.
 (2)证明:连接DM,AM.w w w .x k b 1.c o m
(2)证明:连接DM,AM.w w w .x k b 1.c o m
在等边三角形ABC中,M为BC的中点,
∴  ,
, ,
, .
.
∴  .
.
同理, ,
, .
.
∴  ,
, .
.
∴ △ADM ∽△BEM.
∴  .
.
延长BE交AM于点G,交AD于点K.
∴  ,
, .
.
∴  .
.
∴  .
.
 (3)解:(ⅰ)当△DEF绕点M顺时针旋转
(3)解:(ⅰ)当△DEF绕点M顺时针旋转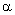 (
(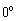 ≤
≤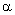 ≤
≤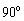 )角时,
)角时,
∵ △ADM ∽△BEM,
∴  .
.
∴ 
∴ 


 .
.
∴  (3≤
(3≤ ≤
≤ ).
).
(ⅱ) 当△DEF绕点M逆时针旋转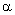 (
(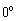 ≤
≤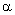 ≤
≤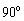 )角时,可证△ADM∽△BEM,
)角时,可证△ADM∽△BEM,
 ∴
∴ 
 .
.
∴  .
.
∴ 


 .
.
∴  (
( ≤
≤ ≤3).
≤3).
综上, (
( ≤
≤ ≤
≤ ).
).

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 的图象如图所示,将其绕坐标原点O旋转
的图象如图所示,将其绕坐标原点O旋转 ,则旋转后的抛物线的解析式为( )
,则旋转后的抛物线的解析式为( )  B.
B.
 D.
D.


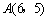 作AB⊥x轴于点B.半径为
作AB⊥x轴于点B.半径为 的⊙A
的⊙A 时,EB的长等于 ;
时,EB的长等于 ;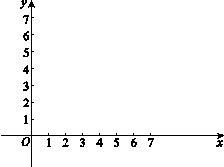
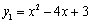 的图象为C1.二次函数
的图象为C1.二次函数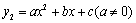 的图象与C1关于y轴对称.
的图象与C1关于y轴对称.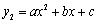 的解析式;
的解析式; 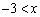 ≤0时,直接写出
≤0时,直接写出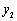 的取值范围;
的取值范围;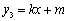 ( k,m为常数,k≠0)的图象经过A,B两点,当
( k,m为常数,k≠0)的图象经过A,B两点,当 时,直接写出x的取值范围.
时,直接写出x的取值范围.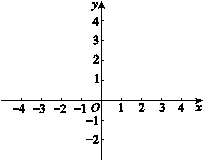
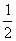 B.
B. 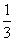 C.
C.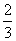 D.
D.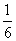
 中,
中, ,如果
,如果 ,那么
,那么 _______°.
_______°. A.40° B.50° C.55° D.80°
A.40° B.50° C.55° D.80° 明和小亮抽得的数字之和所有可能出现的情况.
明和小亮抽得的数字之和所有可能出现的情况.