题目内容
(1)2x2+3x+1=0(用配方法)
(2)(y-4)2=8-2y.
(2)(y-4)2=8-2y.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)根据配方法,可得方程的解;
(2)根据因式分解法,可得方程的解.
(2)根据因式分解法,可得方程的解.
解答:解:(1)移项,得2x2+3x=-1.
系数化为1,得x2+
x=-
.
配方,得x2+
x+
=
,
即(x+
)2=
,
解得x=-
±
,
x1=-
,x2=-1;
(2)移项,得
(y-4)2+2(y-4)=0.
因式分解,得(y-4)[(y-4)+2]=0
y-4=0或y-2=0.
解得y1=4,y2=2.
系数化为1,得x2+
| 3 |
| 2 |
| 1 |
| 2 |
配方,得x2+
| 3 |
| 2 |
| 9 |
| 16 |
| 1 |
| 16 |
即(x+
| 3 |
| 4 |
| 1 |
| 16 |
解得x=-
| 3 |
| 4 |
| 1 |
| 4 |
x1=-
| 1 |
| 2 |
(2)移项,得
(y-4)2+2(y-4)=0.
因式分解,得(y-4)[(y-4)+2]=0
y-4=0或y-2=0.
解得y1=4,y2=2.
点评:本题考查了解一元二次方程,配方法配方时要加一次项系数一半的平方,因式分解法解方程时因式分解是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
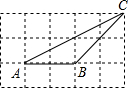 如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )
如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|