题目内容
 如图,直径AB⊥弦CD于E,AE=2cm,CE=4cm.求⊙O半径的长.
如图,直径AB⊥弦CD于E,AE=2cm,CE=4cm.求⊙O半径的长.考点:垂径定理,勾股定理
专题:计算题
分析:设⊙O半径为r,在Rt△OCE中利用勾股定理得42+(r-2)2=r2,然后解方程即可得到⊙O半径的长.
解答:解:设⊙O半径为r,则OE=OA-AE=r-2,
∵AB⊥弦CD,
∴∠CEO=90°,
在Rt△OCE中,∵CE2+OE2=OC2,
∴42+(r-2)2=r2,解得r=5,
即⊙O半径的长为5cm.
∵AB⊥弦CD,
∴∠CEO=90°,
在Rt△OCE中,∵CE2+OE2=OC2,
∴42+(r-2)2=r2,解得r=5,
即⊙O半径的长为5cm.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
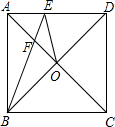 如图,正方形ABCD的边长为2,连接对角线AC、BD交于点O,∠ABD的角平分线交AC于点F,交AD于点E,连接OE,则△OEF的面积为( )
如图,正方形ABCD的边长为2,连接对角线AC、BD交于点O,∠ABD的角平分线交AC于点F,交AD于点E,连接OE,则△OEF的面积为( )A、
| ||||
B、
| ||||
C、3-2
| ||||
D、2
|
某校2013年给希望工程捐款2万元,以后每年都捐款,计划到2015年三年总共捐款6.62万元,若设该校捐款的年平均增长率为x,则可列方程为( )
| A、2+2x2(1+x)=6.62 |
| B、2(1+x)2=6.62 |
| C、2+2(1+x)+2(1+x)2=6.62 |
| D、2(1+x)3=6.62 |
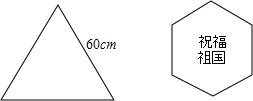 王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )
王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )| A、20cm | B、25cm |
| C、30cm | D、40cm |

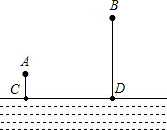 如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.
如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.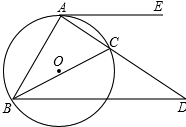 △ABC内接于⊙O,AE切⊙O于A,过B作BD平行AE交AC延长线于D,若AC=4cm CD=3cm,求AB的长.
△ABC内接于⊙O,AE切⊙O于A,过B作BD平行AE交AC延长线于D,若AC=4cm CD=3cm,求AB的长.