题目内容
某海产品市场上现经销一种海产品,已知这种产品的成本价为20元/千克,物价部门限定该种产品的市场售价不得高于32元.经市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=-2x+80.设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式.
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得168元的销售利润,销售价应定为多少元?
(1)求y与x之间的函数关系式.
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得168元的销售利润,销售价应定为多少元?
考点:二次函数的应用,一元二次方程的应用
专题:应用题
分析:(1)根据每天的销售利润=每千克的利润×每天的销量,可得出y与x的函数关系式;
(2)根据(1)所得的函数关系式,利用配方法可得出每天的最大利润.
(3)令y=168,解方程即可得出销售单价.
(2)根据(1)所得的函数关系式,利用配方法可得出每天的最大利润.
(3)令y=168,解方程即可得出销售单价.
解答:解:(1)y=(x-20)w=(x-20)(-2x+80)=-2x2+120x-1600;
(2)y=-2x2+120x-1600=-2(x-30)2+200,
当x=32时,y取得最大值,最大值为200元.
答:当销售价定为30元时,每天的销售利润最大,最大利润是200元.
(3)令y=168,则可得-2x2+120x-1600=168,
解得:x1=28,x2=34(高于物价部门的规定,不符合题意,故舍去).
答:该经销商想要每天获得168元的销售利润,销售价应定为28元/千克.
(2)y=-2x2+120x-1600=-2(x-30)2+200,
当x=32时,y取得最大值,最大值为200元.
答:当销售价定为30元时,每天的销售利润最大,最大利润是200元.
(3)令y=168,则可得-2x2+120x-1600=168,
解得:x1=28,x2=34(高于物价部门的规定,不符合题意,故舍去).
答:该经销商想要每天获得168元的销售利润,销售价应定为28元/千克.
点评:本题考查了二次函数的应用,解答本题的关键是得出y与x的函数关系式,另外要求同学们掌握配方法求最值得应用,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示是一枚质地均匀的骰子的表面展开图,任意投掷这枚骰子,朝上的一面上的数字是恰好等于朝下的一面上的数字的一半的概率为( )
如图所示是一枚质地均匀的骰子的表面展开图,任意投掷这枚骰子,朝上的一面上的数字是恰好等于朝下的一面上的数字的一半的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
在正三角形、等腰梯形、矩形和圆这四种图形中,既是轴对称图形又是中心对称图形的有( )种.
| A、1 | B、2 | C、3 | D、4 |
 在菱形OABC中,A点在反比例函数
在菱形OABC中,A点在反比例函数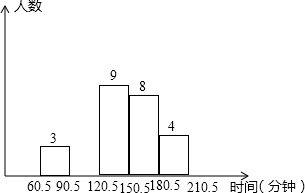 某校为了了解本校九年级学生一天中在家里做作业所用的时间,随机抽查了该校九年级的40名,并把调查所得的所有数据(时间)进行整理,分成五组,绘制成统计图(如图).
某校为了了解本校九年级学生一天中在家里做作业所用的时间,随机抽查了该校九年级的40名,并把调查所得的所有数据(时间)进行整理,分成五组,绘制成统计图(如图).