题目内容
12.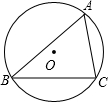 如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.
如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.(1)求证:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R;
(2)若a=5,∠A=60°,求⊙O的半径R.
分析 (1)连接CO并延长交⊙O于D,连接BD,因为∠D=∠A,∠DBC=90°,CD=2R,BC=a,在Rt△BCD中,sinD=$\frac{BC}{2R}$,所以sinA=$\frac{BC}{2R}$=$\frac{a}{2R}$,可得$\frac{a}{sinA}$=2R,同理可证,$\frac{b}{sinB}$=2R,$\frac{c}{sinC}$=2R,由此即可证明.
(2))把a=5,A=60°,代入$\frac{a}{sinA}$=2R,计算即可.
解答 (1)证明:连接CO并延长交⊙O于D,连接BD,
∴∠D=∠A,∠DBC=90°,CD=2R,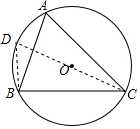 BC=a,
BC=a,
在Rt△BCD中,sinD=$\frac{BC}{2R}$,
∴sinA=$\frac{BC}{2R}$=$\frac{a}{2R}$,
∴$\frac{a}{sinA}$=2R,同理可证,$\frac{b}{sinB}$=2R,$\frac{c}{sinC}$=2R,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R.
(2)∵$\frac{a}{sinA}$=2R,
∴$\frac{5}{\frac{\sqrt{3}}{2}}$=2R,
∴R=$\frac{5\sqrt{3}}{3}$.
点评 本题考查了圆周角定理,直径的性质、锐角三角函数,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
2.在-1、+7、0、-$\frac{2}{5}$、3.14中,正数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.先化简,再求值:($\frac{a-1}{{a}^{2}-4a+4}$-$\frac{a+2}{{a}^{2}-2a}$)÷($\frac{4}{a}$-1),其中a=$\sqrt{3}$+2.
16.若三个不同的有理数的和为0,则下列结论中正确的是( )
| A. | 三个加数全为0 | B. | 至少有两个加数是负数 | ||
| C. | 至少有一个加数是正数 | D. | 至少有两个加数是正数 |
 如图,在半径为1的⊙O中,AB是弦,OM是弦心距,求OM+AB的最大值.
如图,在半径为1的⊙O中,AB是弦,OM是弦心距,求OM+AB的最大值.