题目内容
13.阅读下面的计算过程:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{\sqrt{5}+2}$=$\frac{1×(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}$-2;
…
试求:
(1)$\frac{1}{\sqrt{6}+\sqrt{5}}$的值;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数)的值;
(3)$\frac{2}{1+\sqrt{2}}$+$\frac{2}{\sqrt{2}+\sqrt{3}}$+$\frac{2}{\sqrt{3}+\sqrt{4}}$+…+$\frac{2}{\sqrt{79}+\sqrt{80}}$+$\frac{2}{\sqrt{80}+\sqrt{81}}$…
分析 (1)根据题意可以解答本题;
(2)根据题意可以解答本题;
(3)根据题意可以化简题目中的式子,从而可以解答本题.
解答 解:(1)$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\frac{1×(\sqrt{6}-\sqrt{5})}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}$=$\sqrt{6}-\sqrt{5}$;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$;
(3)$\frac{2}{1+\sqrt{2}}$+$\frac{2}{\sqrt{2}+\sqrt{3}}$+$\frac{2}{\sqrt{3}+\sqrt{4}}$+…+$\frac{2}{\sqrt{79}+\sqrt{80}}$+$\frac{2}{\sqrt{80}+\sqrt{81}}$
=2($\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+…+\sqrt{80}-\sqrt{79}+\sqrt{81}-\sqrt{80}$)
=2×($\sqrt{81}-1$)
=2×(9-1)
=2×8
=16.
点评 本题考查分母有理化,解题的关键是明确分母有理化的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
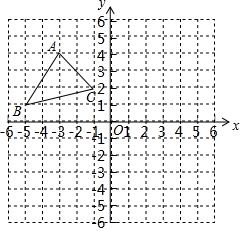 如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(-3,4),B(-5,1),C(-1,2).
如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(-3,4),B(-5,1),C(-1,2).