题目内容
18.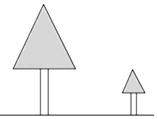 有两棵树,一棵高15米,另一棵高7米,两树相距6米,一只鸟从一棵树的树梢飞到另一棵树的树梢.问小鸟至少飞行10米.
有两棵树,一棵高15米,另一棵高7米,两树相距6米,一只鸟从一棵树的树梢飞到另一棵树的树梢.问小鸟至少飞行10米.
分析 根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
解答  解:如图,设大树高为AB=15m,
解:如图,设大树高为AB=15m,
小树高为CD=7m,
过C点作CE⊥AB于E,则EBDC是矩形,
连接AC,
∴EB=7m,EC=6m,AE=AB-EB=15-7=8m,
在Rt△AEC中,AC=$\sqrt{A{E}^{2}+E{C}^{2}}$=10m,
故小鸟至少飞行10m.
故答案为:10.
点评 本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
相关题目
13.将抛物线y=-x2+1向上平移2个单位,得到的抛物线表达式为( )
| A. | y=-(x+2)2 | B. | y=-(x-2)2 | C. | y=-x2-1 | D. | y=-x2+3 |
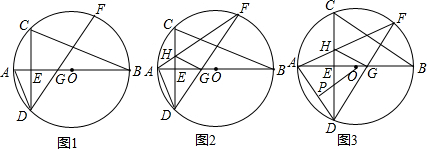

 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
 如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.