题目内容
1. 如图,在△ABC中,∠A=30°,∠B=45°,AC=2,则BC=$\sqrt{2}$.
如图,在△ABC中,∠A=30°,∠B=45°,AC=2,则BC=$\sqrt{2}$.
分析 作CD⊥AB,由AC=2、∠A=30°知CD=1,由∠B=45°知CD=BD=1,最后由勾股定理可得答案.
解答 解:如图,过点C作CD⊥AB于点D,
在Rt△ACD中,∵AC=2,∠A=30°,
∴CD=$\frac{1}{2}$AC=1,
∵在Rt△BCD中,∠B=45°,
∴CD=BD=1,
则BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题主要考查勾股定理、直角三角形的性质,熟练掌握直角三角形的性质和勾股定理是解题的关键.

练习册系列答案
相关题目
9.学校购回一批足球,为检测其质量,从中随机抽取8个足球,记录其质量如下表:
则估计这批足球的平均质量和这组数据的方差分别是( )
| 质量(g) | 410 | 420 | 430 | 440 | 450 |
| 个数 | 2 | 1 | 1 | 3 | 1 |
| A. | 430,20 | B. | 430,200 | C. | 440,30 | D. | 440,300 |
 如图,在△ABC中,∠C=90°,它的周长为(2+$\sqrt{6}$)cm,AB=2cm,求△ABC的面积.
如图,在△ABC中,∠C=90°,它的周长为(2+$\sqrt{6}$)cm,AB=2cm,求△ABC的面积.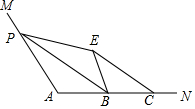 如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=70°.
如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=70°.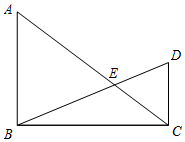 已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=$\frac{3}{5}$,tan∠DBC=$\frac{5}{12}$.
已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=$\frac{3}{5}$,tan∠DBC=$\frac{5}{12}$.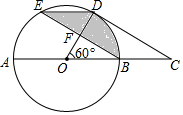 如图,在⊙O中,AB是直径,D、E为⊙O上两点,过点D作⊙O的切线CD交AB的延长线于点C,OD与BE交于F点,四边形BCDE是平行四边形.
如图,在⊙O中,AB是直径,D、E为⊙O上两点,过点D作⊙O的切线CD交AB的延长线于点C,OD与BE交于F点,四边形BCDE是平行四边形.
 如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.
如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.