题目内容
3.先化简,再求值:$\frac{\sqrt{{x}^{2}-2x+1}}{{x}^{2}-x}$-$\frac{1-2x+{x}^{2}}{-1+x}$,其中x=$\frac{1}{\sqrt{3}}$,求代数式的值.
分析 首先化简二次根式以及分式,然后代入求值即可.
解答 解:原式=$\frac{\sqrt{\sqrt{(x-1)^{2}}}}{x(x-1)}$-$\frac{1-x}{x(x-1)}$
=$\frac{1-x}{x(x-1)}$-(x-1)
=-$\frac{1}{x}$-(x-1)
=-$\frac{1}{x}$-x+1,
当x=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$时,原式=-$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+1=1-$\frac{4\sqrt{3}}{3}$.
点评 本题考查了二次根式的化简求值,正确化简二次根式是关键.

练习册系列答案
相关题目
12.近几年安徽省民生事业持续改善,2012年全省民生支出3163亿元,2014年全省民生支出4349亿元,若平均每年民生支出的增长率相同,设这个增长率为x,则下列列出的方程中正确的是( )
| A. | 3163(1+x)2=4349 | B. | 4349(1-x)2=3163 | C. | 3163(1+2x)=4349 | D. | 4349(1-2x)=3163 |
13.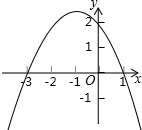 抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )
抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )
 抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )
抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )| A. | x<2 | B. | x>-3 | C. | -3<x<1 | D. | x<-3或x>1 |