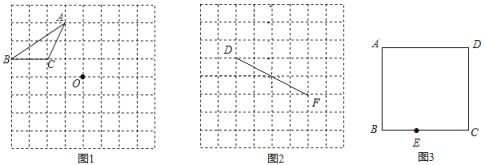
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .若点
.若点![]() 是
是![]() 边上异于点
边上异于点![]() 的另一个点,且
的另一个点,且![]() ,则
,则![]() 的值为______.
的值为______.
【答案】24或36或![]()
【解析】
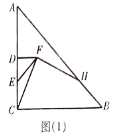
情况1:连接EP交AC于点H,依据先证明![]() 是菱形,再根据菱形的性质可得到∠ECH=∠PCH=60°,然后依据SAS可证明△ECH≌△PCH,则∠EHC=∠PHC=90°,最后依据EP=2EH=2sin60°EC求解即可.
是菱形,再根据菱形的性质可得到∠ECH=∠PCH=60°,然后依据SAS可证明△ECH≌△PCH,则∠EHC=∠PHC=90°,最后依据EP=2EH=2sin60°EC求解即可.
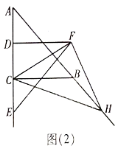
情况2:如图2所示:△ECP为等腰直角三角形,则![]() =
=![]() EC=2
EC=2![]() .此时,
.此时,![]() =24
=24
情况3:如图2:过点P′作P′F⊥BC.通过解直角三角形可以解得FC ,EF,再在Rt△P′EF中,利用勾股定理可以求得![]() .
.
解:情况1:如图所示:连接EP交AC于点H.
∵在![]() 中,
中,![]()
∴![]() 是菱形
是菱形
∵菱形ABCD中,∠B=60°,
∴∠BCD=120°,∠ECH=∠PCH=60°.
在△ECH和△PCH中
 ,
,
∴△ECH≌△PCH.
∴∠EHC=∠PHC=90°,EH=PH.
∴EP=2EH=2sin60°EC=2×![]() ×2
×2![]() =6.
=6.
∴![]() =36
=36
情况2:如图2所示:△ECP为等腰直角三角形,则![]() =
=![]() EC=2
EC=2![]() .
.
∴![]() =24
=24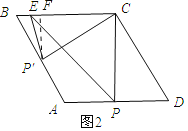
情况3:如图2:过点P′作P′F⊥BC.
∵P′C=2![]() ,BC=4,∠B=60°,
,BC=4,∠B=60°,
∴P′C⊥AB.
∴∠BCP′=30°.
∴FC=![]() ×2
×2![]() =3,P′F=
=3,P′F=![]() ,EF=2
,EF=2![]() -3.
-3.
∴![]() =
=![]()
![]() ,
,
故答案为:24或36或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目