题目内容
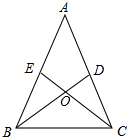 如图△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O.
如图△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O.(1)OB与OC相等吗?请说明你的理由;
(2)点O在∠BAC的平分线上吗?为什么?
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)OB与OC相等.求出CD=BE,∠EBC=∠DCB,证△EBC≌△DCB,推出∠DBC=∠ECB即可.
(2)欲证明O在∠BAC的平分线上,只需推知OE=OD即可.
(2)欲证明O在∠BAC的平分线上,只需推知OE=OD即可.
解答: 解:(1)OB与OC相等.理由如下:
解:(1)OB与OC相等.理由如下:
:∵BD、CE是△ABC的两条中线,
∴CD=
AC,BE=
AB,
∵AB=AC,
∴CD=BE,∠EBC=∠DCB,
在△EBC和△DCB中,
,
∴△EBC≌△DCB(SAS),
∴∠DBC=∠ECB,
∴OB=OC.
(2)由(1)知,△EBC≌△DCB,则BE=CD.
在△BEO与△CDO中,
,
∴△BEO≌△CDO(AAS),
∴OE=OD.
又∵BD⊥AC,CE⊥AB,
∴O在∠BAC的平分线上.
 解:(1)OB与OC相等.理由如下:
解:(1)OB与OC相等.理由如下::∵BD、CE是△ABC的两条中线,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴CD=BE,∠EBC=∠DCB,
在△EBC和△DCB中,
|
∴△EBC≌△DCB(SAS),
∴∠DBC=∠ECB,
∴OB=OC.
(2)由(1)知,△EBC≌△DCB,则BE=CD.
在△BEO与△CDO中,
|
∴△BEO≌△CDO(AAS),
∴OE=OD.
又∵BD⊥AC,CE⊥AB,
∴O在∠BAC的平分线上.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质和判定的应用,关键是推出△EBC≌△DCB,注意:等角对等边.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图,这是函数y=x、y=x2、y=
如图,这是函数y=x、y=x2、y=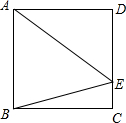 如图,在正方形ABCD中,点E在CD边上,且CE:DE=1:3,求∠AEB的正弦值.
如图,在正方形ABCD中,点E在CD边上,且CE:DE=1:3,求∠AEB的正弦值.