题目内容
一个商人每月将自己的财产增加
,但每月初得从中拿出1000元来维持全家的生活,经过三个月后,发现自已的财产增加了一倍,问商人最初有多少财产?
| 1 |
| 3 |
考点:一元一次方程的应用
专题:
分析:此题先计算出第一个月末此人的资金总数,再减去1000元,将剩余的资金再次按每月增长
,计算第二个月末的资金总数,依次计算至第三个月末的资金总数,而第三个月末的资金总数等于x的2倍,利用此等式解出x的值.
| 1 |
| 3 |
解答:解:设商人最初有x元的财产.
第一个月末此人的资金总数为:x+
x=
x,
减去1000元后的资金为:
x-1000,
第二个月末此人的资金总数为(
x-1000)×
+(
x-1000)=
(
x-1000),
减去1000元后的资金为(
x-1000)×
-1000,
第三个月末此人的资金总数为:[(
x-1000)
-1000]×
+[(
x-1000)
-1000]=[(
x-1000)
-1000]×
,
减去1000元后的资金为[(
x-1000)
-1000]×
-1000,
又他的资金在第三个月后增长了一倍故
[(
x-1000)
-1000]×
-1000=2x,
解得x=11100.
答:商人最初有11100元财产.
第一个月末此人的资金总数为:x+
| 1 |
| 3 |
| 4 |
| 3 |
减去1000元后的资金为:
| 4 |
| 3 |
第二个月末此人的资金总数为(
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
减去1000元后的资金为(
| 4 |
| 3 |
| 4 |
| 3 |
第三个月末此人的资金总数为:[(
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
减去1000元后的资金为[(
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
又他的资金在第三个月后增长了一倍故
[(
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
解得x=11100.
答:商人最初有11100元财产.
点评:此题主要考查一元一次方程在增长率问题上的运用,关键在于明确三年后的资金总数的算法,又由于三年后的资金总数等于x的2倍,列出等量关系,求解方程即可.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
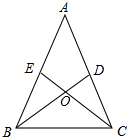 如图△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O.
如图△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O.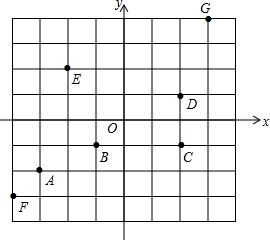 看图完成任务:
看图完成任务: 已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M,若AC=2,BC=1,求CM的长.
已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M,若AC=2,BC=1,求CM的长.