题目内容
两个相似三角形的周长是2：3，它们的面积之差是60cm2，那么它们的面积之和是 ．
考点：相似三角形的性质
专题：
分析：根据相似三角形周长的比等于相似比求出相似比，再根据相似三角形面积的比等于相似比的平分求出面积的比，然后根据比例设出两个三角形的面积，再求解即可．
解答：解：∵两个相似三角形的周长是2：3，
∴它们的相似比为2：3，
∴它们的面积的比为4：9，
设两个三角形的面积分别为4k，9k，
由题意得，9k-4k=60，
解得k=12，
∴两个三角形的面积分别为48cm2，108cm2，
∴它们的面积之和是48+108=156cm2．
故答案为：156cm2．
∴它们的相似比为2：3，
∴它们的面积的比为4：9，
设两个三角形的面积分别为4k，9k，
由题意得，9k-4k=60，
解得k=12，
∴两个三角形的面积分别为48cm2，108cm2，
∴它们的面积之和是48+108=156cm2．
故答案为：156cm2．
点评：本题考查了相似三角形的性质，主要利用了相似三角形的周长的比和面积的比与相似比的关系，熟记性质是解题的关键．
练习册系列答案
相关题目
已知扇形的周长为16，圆心角为
，这个扇形的面积是（ ）
| 360° |
| π |
| A、16π | B、16 | C、32 | D、64 |
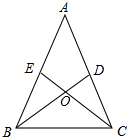如图△ABC中，AB=AC，BD⊥AC于点D，CE⊥AB于点E，BD与CE相交于点O．
已知：如图，点B、C、E三点在同一条直线上，CD平分∠ACE，DB=DA，DM⊥BE于M，若AC=2，BC=1，求CM的长．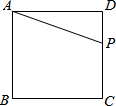
如图，正方形ABCD的边长为4，点P为CD上任意一点（不与C、D重合），设DP=x，四边形ABCP的面积为y．