题目内容
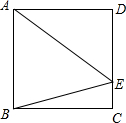如图，在正方形ABCD中，点E在CD边上，且CE：DE=1：3，求∠AEB的正弦值．考点：正方形的性质,勾股定理,锐角三角函数的定义
专题：
分析：过点A作AF⊥BE于F，根据比例设CE=k，DE=3k，得到正方形的边长为4k，利用勾股定理列式求出AE=5k，BE=
k，再求出△ABF和△BCE相似，利用相似三角形对应边成比例列式求出AF，然后根据锐角的正弦等于对边比斜边列式计算即可得解．
| 17 |
解答：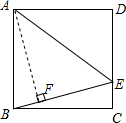
解：如图，过点A作AF⊥BE于F，
∵CE：DE=1：3，
∴设CE=k，DE=3k，
则正方形的边长为4k，
由勾股定理得，AE=
=5k，
BE=
=
k，
∵∠ABF+∠BAF=∠ABF+∠CBE=90°，
∴∠BAF=∠CBE，
又∵∠AFB=∠C=90°，
∴△ABF∽△BCE，
∴
=
，
即
=
，
解得AF=
k，
∴∠AEB的正弦值=
=
=
．
解：如图，过点A作AF⊥BE于F，∵CE：DE=1：3，
∴设CE=k，DE=3k，
则正方形的边长为4k，
由勾股定理得，AE=
| (3k)2+(4k)2 |
BE=
| k2+(4k)2 |
| 17 |
∵∠ABF+∠BAF=∠ABF+∠CBE=90°，
∴∠BAF=∠CBE，
又∵∠AFB=∠C=90°，
∴△ABF∽△BCE，
∴
| AF |
| BC |
| AB |
| BE |
即
| AF |
| 4k |
| 4k | ||
|
解得AF=
16
| ||
| 17 |
∴∠AEB的正弦值=
| AF |
| AE |
| ||||
| 5k |
16
| ||
| 85 |
点评：本题考查了正方形的性质，相似三角形的判定与性质，勾股定理，锐角三角形函数的定义，作辅助线构造出直角三角形和相似三角形是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知MN⊥PQ，垂足为O，点A、A1是以MN为对称轴的对称点，而点A、A2是以PQ为对称点，则点A1A2关于点O成中心对称，你能说明其中的道理吗？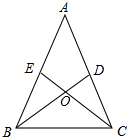
如图△ABC中，AB=AC，BD⊥AC于点D，CE⊥AB于点E，BD与CE相交于点O．
看图完成任务：
已知：如图，点B、C、E三点在同一条直线上，CD平分∠ACE，DB=DA，DM⊥BE于M，若AC=2，BC=1，求CM的长．
如图，点P为△ABC内一点，且PB=AB．求证：AC＞PC．