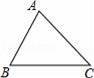
题目内容
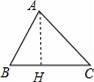
如图,△ABC是锐角三角形,sinC=
 ,则sinA的取值范围是( )
,则sinA的取值范围是( )

A.0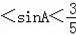
 B.
B.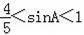
 C.
C.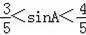
 D.
D.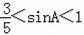

D【考点】锐角三角函数的增减性.
【专题】计算题.
【分析】作AH⊥BC于H,如图,根据正弦定义得到sinC=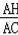
 =
=
 ,则可设AH=4x,AC=5x,利用勾股定理得到CH=3x,所以sin∠HAC=
,则可设AH=4x,AC=5x,利用勾股定理得到CH=3x,所以sin∠HAC=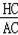
 =
=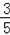
 ,由于∠HAC<∠BAC<90°,然后根据正弦函数为增函数即可得到sin∠BAC的范围.
,由于∠HAC<∠BAC<90°,然后根据正弦函数为增函数即可得到sin∠BAC的范围.
【解答】解:作AH⊥BC于H,如图,
在Rt△ABH中,sinC=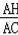
 =
=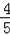
 ,
,
设AH=4x,AC=5x,
所以CH=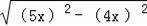
 =3x,
=3x,
所以sin∠HAC=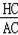
 =
=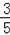
 ,
,
∵∠HAC<∠BAC<90°,
∴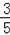
 <sin∠BAC<1.
<sin∠BAC<1.
故选D.

【点评】本题考查了锐角三角函数的增减性:锐角三角函数值都是正值;当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大);当角度在0°≤∠A≤90°间变化时,0≤sinA≤1,1≥cosA≥0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





 的解是 .
的解是 .

 (ab≠0),那么下列比例式变形正确的是( )
(ab≠0),那么下列比例式变形正确的是( ) B.
B. C.
C. D.
D.