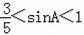题目内容
在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.
(1)若BC=5,AC=12,PD⊥AB,求AP的长;
(2)当AD=PE时,求证:四边形BDEP为菱形;
(3)若BC=5,∠A=30°,P点从C点运动到A点,在这个过程中,求E点所经过的路径长.

【考点】四边形综合题.
【分析】(1)根据勾股定理求出AB,根据相似三角形的判定定理证明△ADP∽△ACB,根据相似三角形的性质得到比例式,计算即可;
(2)根据四条边相等的四边形是菱形证明即可;
(3)根据等边三角形的性质和平角的定义求出P点从C点运动到A点E点运动的圆心角,根据弧长公式计算即可.
【解答】(1)解:∵∠C=90°,BC=5,AC=12,
∴AB=
 =13,
=13,
∵PD⊥AB,∠C=90°,
∴△ADP∽△ACB,
∴
 =
=
 ,即
,即
 =
=
 ,
,
解得,AP=
 ;
;
(2)证明:由翻折变换的性质可知,PB=PE,DB=DE,
∵AD=PE,BD=AD,
∴BP=PE=ED=DB,
∴四边形BDEP为菱形;
(3)∵BC=5,∠A=30°,
∴AB=2BC=10,
∴DE=BD=
 AB=5,
AB=5,
当P点与C点重合时,△BPD是等边三角形,
∴∠BDP=60°,
∴∠EDP=60°,
∴∠EDA=60°,
当P点与A点重合时,∠EDA=180°,
∴P点从C点运动到A点E点运动的圆心角为60°+180°=240°,

 =
=
 ,
,
∴E点所经过的路径长为
 .
.
【点评】本题考查的是菱形的判定、弧长的计算、翻折变换的性质,掌握四条边相等的四边形是菱形、弧长的计算公式是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.

 ,则sinA的取值范围是( )
,则sinA的取值范围是( )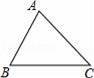

 B.
B.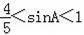
 C.
C.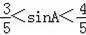
 D.
D.