题目内容
如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
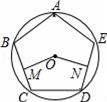

A.108° B.144° C.150° D.166°
B【考点】正多边形和圆.
【分析】由垂径定理得出∠OMC=∠OND=90°,由正五边形的性质得出∠C=∠D=108°,由五边形内角和即可求出结果.
【解答】解:∵点M为BC中点,点N为DE中点,
∴OM⊥BC,ON⊥DE,
∴∠OMC=∠OND=90°,
∵五边形ABCDE是正五边形,
∴∠C=∠D=(5﹣2)×180°÷5=108°,
∴∠MON=(5﹣2)×180°﹣2×90°﹣2×108°=144°;
故选:B.
【点评】本题考查了正五边形的性质、垂径定理;熟练掌握正五边形的性质,由垂径定理得出∠OMC=∠OND=90°是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,把△EFO 缩小,若 E(-4, 2) ,则点 E 的对应点 E ' 的坐标是( )
,把△EFO 缩小,若 E(-4, 2) ,则点 E 的对应点 E ' 的坐标是( )
 B.
B.
 C.
C.
 D.
D.


 D.﹣
D.﹣
 ,则sinA的取值范围是( )
,则sinA的取值范围是( )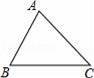

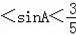
 B.
B.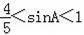
 C.
C.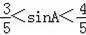
 D.
D.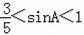
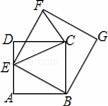

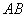 是⊙
是⊙ 的直径,点
的直径,点 在
在 ,若
,若 ,
, ( ).
( ).