题目内容
13.已知点($\frac{1}{2}$,y1),(2,y2),(3,y3)都在函数y=a(x-1)2+3(a<0)图象上,则( )| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
分析 由函数的解析式可知抛物线的对称轴为x=1,然后由抛物线的对称性可知:当x=1.5时,y=y1然后由抛物线的增减性判断即可.
解答 解:由题意可知:抛物线的对称轴为x=1,
由抛物线的对称性可知($\frac{3}{2}$,y1),
∵a<0,
∴在对称轴的右侧y随x的增大而减小.
∵$\frac{3}{2}<2<3$,
∴y3<y2<y1.
故选:C.
点评 本题主要考查的是二次函数的性质、掌握二次函数的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在△ABC中,已知b=6,c=10,B=30°,则解此三角形的结果是( )
| A. | 无解 | B. | 一解 | ||
| C. | 两解 | D. | 解的个数不能确定 |
18. 左边圆锥体的俯视图是( )
左边圆锥体的俯视图是( )
 左边圆锥体的俯视图是( )
左边圆锥体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
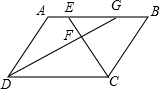 如图:?ABCD中,∠ΒCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G,求证:AE=BG.
如图:?ABCD中,∠ΒCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G,求证:AE=BG.