题目内容
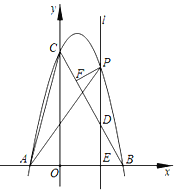
【题目】直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,点
,点![]() ,与坐标轴分别交于点
,与坐标轴分别交于点![]() 和点
和点![]() ,
,![]() .
.
(1)求直线![]() 的解析式.
的解析式.
(2)在![]() 轴上求出点
轴上求出点![]() ,使以
,使以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【答案】(1)![]() .(2)点
.(2)点![]() 坐标为
坐标为![]() ,或
,或![]() .
.
【解析】
(1)将![]() 代入双曲线,求出
代入双曲线,求出![]() ,即得
,即得![]() .作
.作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,根据平行线分线段成比例,可得
,根据平行线分线段成比例,可得![]() . 将
. 将![]() 代入双曲线,求出
代入双曲线,求出![]() 的值,即得
的值,即得![]() .利用待定系数法直接求出直线
.利用待定系数法直接求出直线![]() 的解析式.
的解析式.
(2)分两种情况讨论,①当![]() ∽
∽![]() ,即
,即![]() 与
与![]() 重合时,②当
重合时,②当![]() ∽
∽![]() 时,即是
时,即是![]() ⊥
⊥![]() 可得
可得![]() ∽
∽![]() ,结合已知先求出
,结合已知先求出![]() 的长,再求出
的长,再求出![]() 的长,继而求出
的长,继而求出![]() 的长,即可求出点
的长,即可求出点![]() 的坐标.
的坐标.
(1)解:将![]() 代入双曲线,得
代入双曲线,得![]() .
.
∴![]() . ∴
. ∴![]() .
.
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]()
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
将![]() 代入双曲线,得
代入双曲线,得![]() .
.
∴![]() . ∴
. ∴![]() .
.
将![]() ,
,![]() 代入直线,得
代入直线,得 ![]()
解得![]() ,
,![]()
直线![]() 的解析式为 y=
的解析式为 y=![]() ;
;
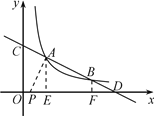
(2)解:如图,①由(1),点![]() 符合。
符合。
![]() , ∴
, ∴![]() ∽
∽![]() .
.
此时![]() .
.
②当![]() 时,
时,![]() ∽
∽![]() .
.
此时,![]() ∽
∽![]() .
.
∴![]() .
.![]() .
.
![]() ,∴
,∴![]() .
.
由![]() ,得
,得![]() .
.
∴![]() ∴
∴![]() ∴
∴![]() .
.
∴![]() ∴
∴![]() ∴
∴![]() .
.
∴![]() .
.
综上,满足条件的点![]() 坐标为
坐标为![]() ,或
,或![]() .
.
故答案为:(1)![]() .(2)点
.(2)点![]() 坐标为
坐标为![]() ,或
,或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目