题目内容
17. 如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.(1)求证:△BEC≌△CDB;
(2)若∠A=50°,BE⊥AC,求∠BCD的度数.
分析 (1)根据全等三角形的性质得到AB=AC,AD=AE,BE=CD,根据全等三角形的判定定理即可得到结论;
(2)根据等腰三角形的性质和三角形的内角和得到∠ACB=∠ABC=65°,根据垂直的定义得到∠BEC=∠AEB=90°,于是得到结论.
解答 (1)证明: ∵△ABE≌△ACD,
∵△ABE≌△ACD,
∴AB=AC,AD=AE,BE=CD,
∴BD=CE,
在△BEC与△CDB中,$\left\{\begin{array}{l}{BD=CE}\\{CD=BE}\\{BC=CB}\end{array}\right.$,
∴△BEC≌△CDB;
(2)解:∵AB=AC,∠A=50°,
∴∠ACB=∠ABC=65°,
∵BE⊥AC,
∴∠BEC=∠AEB=90°,
∴∠ABE=∠ACD=40°,
∴∠BCD=15°.
点评 本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
7.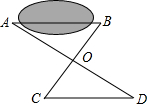 要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
 要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )| A. | OA=OD,OB=OC | B. | ∠B=∠C,OB=OC | C. | ∠B=∠C,OA=OD | D. | ∠C=∠B,∠A=∠D |
6.一元二次方程3x(x+1)=3x+3的解为( )
| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-1 | D. | x1=0,x2=-1 |
 如图,等腰△ABC中,∠CAB=∠CBA,点C、D、E在直线l上,且∠ADC=∠ACB=∠BEC.
如图,等腰△ABC中,∠CAB=∠CBA,点C、D、E在直线l上,且∠ADC=∠ACB=∠BEC.