题目内容
6. 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )| A. | 10$\sqrt{3}$米 | B. | 15米 | C. | 20$\sqrt{3}$米 | D. | 30米 |
分析 作AM⊥BC于M,设AM=x,先证明PB=AB=2x,在RT△PBH中利用sin∠PBH=$\frac{PH}{PB}$解决问题.
解答 解:如图作AM⊥BC于M,设AM=x.
∵tan∠ABM=$\frac{\sqrt{3}}{3}$,
∴∠ABM=30°,
∴AB=2AM=2x,
∵∠HPB=30°,
∴∠PBH=90°-∠HPB=60°,
∴∠ABP=180°-∠PBH-∠ABM=90°,
∴∠BPA=∠BAP=45°,
∴AB=BP=2x,
在Rt△PBH中,∵sin∠PBH=$\frac{PH}{PB}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{30}{2x}$,
∴x=10$\sqrt{3}$.
故选:A.
点评 本题考查解直角三角形、直角三角形30度角的性质等知识,解题的关键是理解坡度、俯角、仰角的概念,学会转化的思想,把问题转化为解直角三角形,属于中考常考题型.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
1.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.已知函数y=3x2-6x+k(k为常数)图象经过点A(2,y1),B(3,y2),C(4,y3),则有( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |
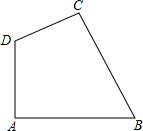 如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.
如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.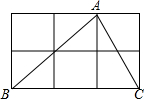 如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形共有3个(不含△ABC).
如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形共有3个(不含△ABC).