题目内容
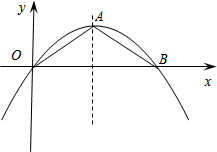 如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.(1)求抛物线的解析式;
(2)在y轴上有一点M使△MAB的周长最小,求出此时△MAB的周长;
(3)在(2)的条件下,在抛物线上是否存在点N(不与点O、A重合),使∠NAO比∠MAO小?若存在请求出点N横坐标xN的取值范围;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)已知了抛物线的顶点坐标,可将其解析式设为顶点坐标式,然后将原点坐标代入上式,即可求得待定系数的值,从而确定该抛物线的解析式.
(2)作B关于y轴的对称点B′(-4,0),连接AB′交y轴于M,则M即为所求的点,此时△MAB的周长最小,根据△MAB的周长=MA+MB+AB=AB′+AB即可求得.
(3)求得∠NAO=∠MAO时的N的坐标有两个,根据两个交点的坐标即可求得.
(2)作B关于y轴的对称点B′(-4,0),连接AB′交y轴于M,则M即为所求的点,此时△MAB的周长最小,根据△MAB的周长=MA+MB+AB=AB′+AB即可求得.
(3)求得∠NAO=∠MAO时的N的坐标有两个,根据两个交点的坐标即可求得.
解答: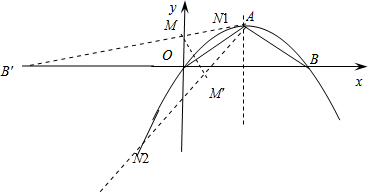 解:(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,
解:(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,
∵抛物线过原点,
∴a(0-2)2+1=0,a=-
;
∴抛物线的解析式为y=-
(x-2)2+1=-
x2+x.
(2)由(1)可知B(4,0),作B关于y轴的对称点B′(-4,0),连接AB′交y轴于M,则M即为所求的点,此时△MAB的周长最小,
∴此时△MAB的周长=MA+MB+AB=AB′+AB=
+
=
+
.
(3)设直线AB′的解析式为y=kx+b,
∴
,解得
,
∴直线AB′的解析式为y=
x+
,
设直线y=
x+
与抛物线的交点N1,
∴
,解得
,
∴N1(
,
);
过M作MG⊥OA于G,
∵直线AB′的解析式为y=
x+
,
∴M(0,
0
∵直线OA的解析式为y=
x,
∴直线MG的解析式为y=-2x+
,
∴G(
,
),
作M关于OA的对称点M′,则G为MM′的中点,
∴M′(
,-
),
∴直线AM′的解析式为y=
x-
,
此时∠MAO=∠M′AO,
解
得
,
∴直线AM′和抛物线的交点N2(-
,-
),
∴满足条件的N点在N1与N2之间,(原点除外),
∴-
<xN<
且xN≠0.
 解:(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,
解:(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,∵抛物线过原点,
∴a(0-2)2+1=0,a=-
| 1 |
| 4 |
∴抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)由(1)可知B(4,0),作B关于y轴的对称点B′(-4,0),连接AB′交y轴于M,则M即为所求的点,此时△MAB的周长最小,
∴此时△MAB的周长=MA+MB+AB=AB′+AB=
| (2+4)2+12 |
| (4-2)2+12 |
| 37 |
| 5 |
(3)设直线AB′的解析式为y=kx+b,
∴
|
|
∴直线AB′的解析式为y=
| 1 |
| 6 |
| 2 |
| 3 |
设直线y=
| 1 |
| 6 |
| 2 |
| 3 |
∴
|
|
∴N1(
| 4 |
| 3 |
| 8 |
| 9 |
过M作MG⊥OA于G,
∵直线AB′的解析式为y=
| 1 |
| 6 |
| 2 |
| 3 |
∴M(0,
| 2 |
| 3 |
∵直线OA的解析式为y=
| 1 |
| 2 |
∴直线MG的解析式为y=-2x+
| 2 |
| 3 |
∴G(
| 4 |
| 15 |
| 2 |
| 15 |
作M关于OA的对称点M′,则G为MM′的中点,
∴M′(
| 8 |
| 15 |
| 2 |
| 5 |
∴直线AM′的解析式为y=
| 21 |
| 22 |
| 10 |
| 11 |
此时∠MAO=∠M′AO,
解
|
|
∴直线AM′和抛物线的交点N2(-
| 20 |
| 11 |
| 320 |
| 121 |
∴满足条件的N点在N1与N2之间,(原点除外),
∴-
| 20 |
| 11 |
| 4 |
| 3 |
点评:本题考查了待定系数法求解析式,轴对称-最短路线问题,直线和抛物线的交点问题,(3)求得交点坐标是本题的难点和关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
在下列数
,-
,0.55,π,
,1.211211121…(每两个2之间多一个1)中,无理数的个数有( )
| 9 |
| 18 |
| 7 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列计算正确的是( )
| A、-2-1=-1 | ||
| B、-(-2)3=8 | ||
C、3÷
| ||
| D、(-2)4=8 |
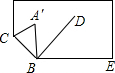 如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )
如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )| A、90° | B、80° |
| C、100° | D、70° |
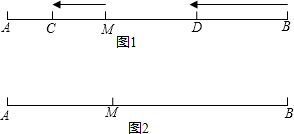 如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.
如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示. 已知二次函数y=-x2+(m-1)x+m.
已知二次函数y=-x2+(m-1)x+m.