题目内容
5.若关于x的方程x2+2x+m=0有两个不相等的实数根,则m的取值范围在数轴上表示正确的是( )| A. | 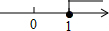 | B. | 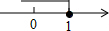 | C. | 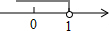 | D. | 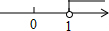 |
分析 根据已知得出22-4×1×m>0,求出不等式的解集,最后在数轴上表示出来,即可得出选项.
解答 解:∵关于x的方程x2+2x+m=0有两个不相等的实数根,
∴22-4×1×m>0,
解得:m<1,
在数轴上表示为: ,
,
故选C.
点评 本题考查了在数轴上表示不等式的解集,根的判别式的应用,注意:一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
13.下列方程中,是一元二次方程的是( )
| A. | 4x2=3y | B. | x(x+1)=5x2-1 | C. | $\sqrt{x}$-3=5x2-$\sqrt{6}$ | D. | $\frac{1}{{x}^{2}}$+3x-1=0 |
17.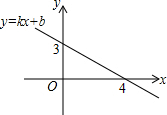 已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )
已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )
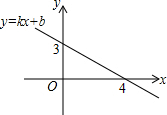 已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )
已知一次函数y=kx+b(k、b为常数)的图象如图所示,那么关于x的不等式kx+b>0的解集是( )| A. | x>3 | B. | x>4 | C. | x<3 | D. | x<4 |
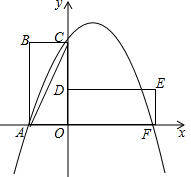 如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.
如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.