题目内容
 如图,矩形OABC放置在第一象限内,已知A(3,0),∠AOB=30°,反比例函数y=
如图,矩形OABC放置在第一象限内,已知A(3,0),∠AOB=30°,反比例函数y=| k |
| x |
(1)若点D为BC的中点,试证明点E为AB的中点;
(2)若点A关于直线OB的对称点为F,试探究:点F是否落在该双曲线上?
考点:反比例函数图象上点的坐标特征
专题:
分析:(1)根据直角三角形的性质,可得AB的长,根据矩形的性质,可得D点的坐标,根据待定系数法,可得反比例函数解析式,根据图象上的点满足函数解析式,可得证明结论;
(2)根据对称的性质,可得∠AOF的大小,OF与OA的关系,根据直角三角形的性质,可得F点的坐标,根据F点纵横坐标的乘积与反比例函数解析式中k的值,可得答案.
(2)根据对称的性质,可得∠AOF的大小,OF与OA的关系,根据直角三角形的性质,可得F点的坐标,根据F点纵横坐标的乘积与反比例函数解析式中k的值,可得答案.
解答:(1)证明:∵OA=3,∠AOB=30°,
∴AB=
.
∵D点D为BC的中点,
∴D(1.5,
).
∴反比例函数解析式是y=
.
当xE=3时,yE=
,
∴E为AB的中点;
(2)作FG⊥OA于点G,如图: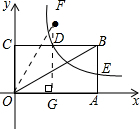 ,
,
∵点A的对称点为,
∴∠AOF=60°.
∵OF=OA=3,
∴OG=
,FG=
.
∴F(
,
).
∵
×
≠
,
∴点F没有落在双曲线上.
∴AB=
| 3 |
∵D点D为BC的中点,
∴D(1.5,
| 3 |
∴反比例函数解析式是y=
3
| ||
| 2x |
当xE=3时,yE=
| ||
| 2 |
∴E为AB的中点;
(2)作FG⊥OA于点G,如图:
 ,
,∵点A的对称点为,
∴∠AOF=60°.
∵OF=OA=3,
∴OG=
| 3 |
| 2 |
3
| ||
| 2 |
∴F(
| 3 |
| 2 |
3
| ||
| 2 |
∵
| 3 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
∴点F没有落在双曲线上.
点评:本题考查了反比例函数图象上点的坐标特征,利用待定系数法求解析式,图象上的点满足函数解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.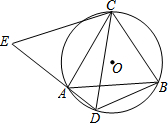 如图,△ABC是⊙O的内接三角形,AC=BC,点D是⊙O中弧AB的上的一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,点D是⊙O中弧AB的上的一点,延长DA至点E,使CE=CD.
 如图,在Rt△ABC中,∠C=90°,AB=26cm,sinA=
如图,在Rt△ABC中,∠C=90°,AB=26cm,sinA=