题目内容
1. 如图,P是△ABC的∠ABC和∠ACB的外角的平分线的交点,若∠A=90°,则∠P=45°.
如图,P是△ABC的∠ABC和∠ACB的外角的平分线的交点,若∠A=90°,则∠P=45°.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和列式表示出∠ACE和∠PCE,再根据角平分线的定义表示出∠PBC和∠PCE,然后整理求出∠A=2∠P,再代入进行计算即可得解.
解答 解:根据三角形的外角性质,∠ACE=∠A+∠ABC,∠PCE=∠P+∠PBC,
∵BP平分∠ABC,CP是△ABC的外角的平分线,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCE=$\frac{1}{2}$∠ACE,
∴∠P+$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠A+∠ABC),
∴∠A=2∠P,
∵∠A=90°,
∴∠P=45°
故答案为:45°
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,准确识图并求出∠A=2∠P是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
12. 如图,在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,若S△ADE=S四边形DBCE,则AD:DB等于( )
如图,在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,若S△ADE=S四边形DBCE,则AD:DB等于( )
 如图,在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,若S△ADE=S四边形DBCE,则AD:DB等于( )
如图,在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,若S△ADE=S四边形DBCE,则AD:DB等于( )| A. | 1:$\sqrt{2}$ | B. | 1:1 | C. | 1:($\sqrt{2}-1$) | D. | $\sqrt{2}$:1 |
16.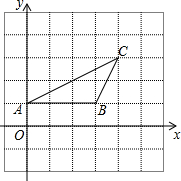 如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
 如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
如图,在平面直角坐标系中,若△ABC三点坐标分别为A(0,1),B(3,1),C(4,3),如果要找一点D,使△ABD与△ABC全等,那么点D的坐标是(4,-1)或(-1,3)或(-1,-1).
6. 如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AB=CD | C. | ∠M=∠N | D. | ∠A=∠NCD |
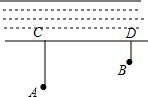 如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.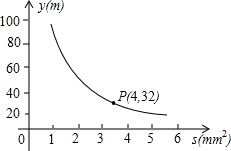 兰州是拉面的故乡,在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示,若工人师傅将面团拉成160根,每根长0.5m时为成品,则此时拉面粗1.6mm2.
兰州是拉面的故乡,在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示,若工人师傅将面团拉成160根,每根长0.5m时为成品,则此时拉面粗1.6mm2.