题目内容
 如图,在⊙O中直径CD垂直弦AB,垂足为E,若∠AOD=52°,则∠DCB=
如图,在⊙O中直径CD垂直弦AB,垂足为E,若∠AOD=52°,则∠DCB=考点:圆周角定理,垂径定理
专题:
分析:连接OB,先根据直径CD垂直弦AB得出
=
,故可得出∠BOE=∠AOE,由圆周角定理即可得出结论.
 |
| AD |
 |
| BD |
解答: 解:连接OB,
解:连接OB,
∵直径CD垂直弦AB,
∴
=
,
∴∠BOE=∠AOE=52°,
∴∠DCB=
∠BOE=26°.
答案为:26°.
 解:连接OB,
解:连接OB,∵直径CD垂直弦AB,
∴
 |
| AD |
 |
| BD |
∴∠BOE=∠AOE=52°,
∴∠DCB=
| 1 |
| 2 |
答案为:26°.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
 如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )
如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )| A、20° | B、25° |
| C、30° | D、35° |
估算实数
的大小时,若使误差小于1,则结果应为( )
| 3 | 90 |
| A、3或4 | B、4或5 |
| C、5或6 | D、9或10 |
 如图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形,则这些相同的小正方体的个数( )
如图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形,则这些相同的小正方体的个数( )| A、4 | B、5 | C、6 | D、7 |
 如图,
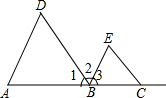
如图, 如图所示,已知∠1=∠2,DE∥BC,你能判断出图形中还有哪些角是相等的吗?(写出两对相等角即可)
如图所示,已知∠1=∠2,DE∥BC,你能判断出图形中还有哪些角是相等的吗?(写出两对相等角即可) 如图,若∠1+∠2=∠3,则∠2+∠4=180°,请说明理由.
如图,若∠1+∠2=∠3,则∠2+∠4=180°,请说明理由.