题目内容
用配方法证明：代数式4x2+y2-4x+6y+11恒大于零．
考点：配方法的应用,非负数的性质：偶次方
专题：证明题
分析：利用完全平方公式分别分解因式，再利用偶次方的性质进而得出即可．
解答：证明：4x2+y2-4x+6y+11=（2x-1）2+（y+3）2+1，
∵（2x-1）2≥0，（y+3）2≥0，
∴原式=（2x-1）2+（y+3）2+1＞0，
即代数式4x2+y2-4x+6y+11恒大于零．
∵（2x-1）2≥0，（y+3）2≥0，
∴原式=（2x-1）2+（y+3）2+1＞0，
即代数式4x2+y2-4x+6y+11恒大于零．
点评：此题主要考查了配方法的应用，熟练应用完全平方公式是解题关键．
练习册系列答案
相关题目
如图，AD是△ABC的中线，
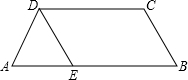如图，已知DC∥AB，∠C=∠DEB，求证：DE∥BC．
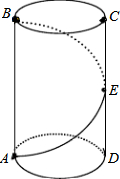一只螳螂在松树树干的A点处，发现它的正上方B点处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是按如图所示的路线，绕到虫子后面吃掉它．已知树干的半径为10cm，A、B两点的距离为40cm．（其中π取3）
如图，∠B=∠C，D在BC上，∠BAD=30°，在AC上取AE=AD，∠ADE=∠AED，求∠EDC的度数．