题目内容
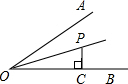 如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C.若OC=2,则PC的长是
如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C.若OC=2,则PC的长是考点:含30度角的直角三角形,勾股定理,矩形的判定与性质
专题:计算题
分析:延长CP,与OA交于点Q,过P作PD⊥OA,利用角平分线定理得到PD=PC,在直角三角形OQC中,利用锐角三角函数定义求出QC的长,在直角三角形QDP中,利用锐角三角函数定义用PD(即PC)表示出PQ,由QP+PC=QC,求出PC的长即可.
解答: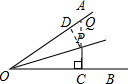 解:延长CP,与OA交于点Q,过P作PD⊥OA,
解:延长CP,与OA交于点Q,过P作PD⊥OA,
∵OP平分∠AOB,PD⊥OA,PC⊥OB,
∴PD=PC,
在Rt△QOC中,∠AOB=30°,OC=2,
∴QC=OCtan30°=2×
=
,∠APD=30°,
在Rt△QPD中,cos30°=
=
,即PQ=
DP=
PC,
∴QC=PQ+PC,即
PC+PC=
,
解得:PC=4-2
.
故答案为:4-2
 解:延长CP,与OA交于点Q,过P作PD⊥OA,
解:延长CP,与OA交于点Q,过P作PD⊥OA,∵OP平分∠AOB,PD⊥OA,PC⊥OB,
∴PD=PC,
在Rt△QOC中,∠AOB=30°,OC=2,
∴QC=OCtan30°=2×
| ||
| 3 |
2
| ||
| 3 |
在Rt△QPD中,cos30°=
| DP |
| PQ |
| ||
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
∴QC=PQ+PC,即
2
| ||
| 3 |
2
| ||
| 3 |
解得:PC=4-2
| 3 |
故答案为:4-2
| 3 |
点评:此题考查了含30度直角三角形的性质,锐角三角函数定义,熟练掌握直角三角形的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知A、C两地相距40千米,B、C两地相距50千米,甲乙两车分别从A、B两地同时出发到C地.若乙车每小时比甲车多行驶12千米,则两车同时到达C地.设乙车的速度为x千米/小时,依题意列方程正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
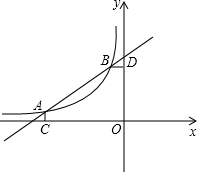 如图,已知A(-4,
如图,已知A(-4, 画出函数y1=-x+1,y2=2x-5的图象,利用图象回答下列问题:
画出函数y1=-x+1,y2=2x-5的图象,利用图象回答下列问题: 在△ABC中,过三角形的三个顶点A、B、C向它的对边作垂线,垂足分别为D、E、F,若AC=5cm,BE=6cm,求△ABC的面积.
在△ABC中,过三角形的三个顶点A、B、C向它的对边作垂线,垂足分别为D、E、F,若AC=5cm,BE=6cm,求△ABC的面积. 一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次越野跑的全程为
一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚所跑的路程y(米)与时间t(秒)之间的函数关系如图,则这次越野跑的全程为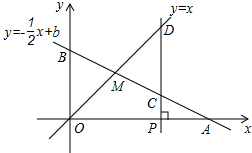 如图,已知函数y=-
如图,已知函数y=-