题目内容
 正五边形ABCDE内接于⊙O,连接AC,AD.
正五边形ABCDE内接于⊙O,连接AC,AD.(1)求证:CD2=AC2-AC•CD.
(2)求
| CD |
| AC |
考点:正多边形和圆
专题:
分析:(1)连接BD,先根据SAS定理得出△ABC≌△BCD故可得出AC=BD,∠BAC=∠BCA=∠CBD=∠CDB,再由相似三角形的判定定理得出△ABC∽△BFC,由相似三角形的对应边成比例即可得出结论;
(2)由(1)知∠CDF=∠CAD=36°,AF=CD,故△CDF∽△CAD,由△ACD是黄金三角形,故可得出结论.
(2)由(1)知∠CDF=∠CAD=36°,AF=CD,故△CDF∽△CAD,由△ACD是黄金三角形,故可得出结论.
解答: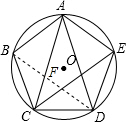 (1)证明:连接BD,
(1)证明:连接BD,
∵是正五边形ABCDE,
∴∠ABC=∠BCD=108°,AB=BC=CD.
在△ABC△BCD中,
,
∴△ABC≌△BCD(SAS)
∴AC=BD,∠BAC=∠BCA=∠CBD=∠CDB=36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°,
∠AFB=∠ACB+∠CBD=36°+36°=72°,
∴∠ABF=∠AFB,
∴AB=AF.
∵∠BAC=∠FBC=36°,∠ACB=∠BCF,
∴△ABC∽△BFC,
∴
=
,
∴BC2=AC×CF.
∵BC=CD,CF=AC-AF=AC-CD,
∴CD2=AC×(AC-CD)=AC2-AC×CD.
(2)∵由(1)知∠CDF=∠CAD=36°,AF=CD,
∴△CDF∽△CAD,
∴
=
,即CD2=AC•CF,
∴△ACD是黄金三角形,
∴
=
.
 (1)证明:连接BD,
(1)证明:连接BD,∵是正五边形ABCDE,
∴∠ABC=∠BCD=108°,AB=BC=CD.
在△ABC△BCD中,
|
∴△ABC≌△BCD(SAS)
∴AC=BD,∠BAC=∠BCA=∠CBD=∠CDB=36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°,
∠AFB=∠ACB+∠CBD=36°+36°=72°,
∴∠ABF=∠AFB,
∴AB=AF.
∵∠BAC=∠FBC=36°,∠ACB=∠BCF,
∴△ABC∽△BFC,
∴
| BC |
| CF |
| AC |
| BC |
∴BC2=AC×CF.
∵BC=CD,CF=AC-AF=AC-CD,
∴CD2=AC×(AC-CD)=AC2-AC×CD.
(2)∵由(1)知∠CDF=∠CAD=36°,AF=CD,
∴△CDF∽△CAD,
∴
| CD |
| AC |
| CF |
| CD |
∴△ACD是黄金三角形,
∴
| CD |
| AC |
| ||
| 2 |
点评:本题考查的是正多边形和圆,熟知正五边形的性质及黄金三角形的定义是解答此题的关键.

练习册系列答案
相关题目
 已知⊙O和⊙O上的一点A.
已知⊙O和⊙O上的一点A.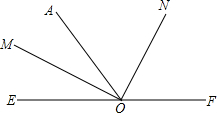 如图所示,若∠AOE和∠AOF是两个相邻的角,OM、ON分别是∠AOE和∠AOF的平分线,∠MON=90°,问:E、O、F三点在同一条直线上吗?若在,请说明理由.
如图所示,若∠AOE和∠AOF是两个相邻的角,OM、ON分别是∠AOE和∠AOF的平分线,∠MON=90°,问:E、O、F三点在同一条直线上吗?若在,请说明理由.