题目内容
 已知⊙O和⊙O上的一点A.
已知⊙O和⊙O上的一点A.(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题的作图中,如果点E在弧AD上,求证:DE是⊙O内接正十二边形的一边.
考点:正多边形和圆
专题:
分析:(1)根据圆内接正多边形的作法画出图形即可;
(2)先求出∠DOE的度数,进而可得出结论.
(2)先求出∠DOE的度数,进而可得出结论.
解答: (1)解:作法:
(1)解:作法:
①作直径AC;
②作直径BD⊥AC;
③依次连结A、B、C、D四点,
四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心,以OA长为半径作弧,交⊙O于E、H、F、G;
⑤顺次连结A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形.
(2)证明:连结OE、DE.
∵∠AOD=
=90°,∠AOE=
=60°,
∴∠DOE=∠AOD-∠AOE=90°-60°=30°.
∴DE为⊙O的内接正十二边形的一边.
 (1)解:作法:
(1)解:作法:①作直径AC;
②作直径BD⊥AC;
③依次连结A、B、C、D四点,
四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心,以OA长为半径作弧,交⊙O于E、H、F、G;
⑤顺次连结A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形.
(2)证明:连结OE、DE.
∵∠AOD=
| 360° |
| 4 |
| 360° |
| 6 |
∴∠DOE=∠AOD-∠AOE=90°-60°=30°.
∴DE为⊙O的内接正十二边形的一边.
点评:本题考查的是正多边形和圆,熟知圆内接正四边形及正六边形的作法是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下边给出的是2005年4月份的日历,任意圈出一竖列上相邻的三个数,请运用方程的思想来研究,你发现这三个数的和不可能是( )


| A、69 | B、50 | C、42 | D、57 |
 如图,反比例函数y1=
如图,反比例函数y1=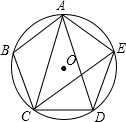 正五边形ABCDE内接于⊙O,连接AC,AD.
正五边形ABCDE内接于⊙O,连接AC,AD. 如图所示的直角坐标系中,正方形ABCD的各个顶点的坐标分别是A(1,5),B(5,4),C(4,0),D(0,1)
如图所示的直角坐标系中,正方形ABCD的各个顶点的坐标分别是A(1,5),B(5,4),C(4,0),D(0,1)