题目内容
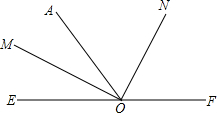 如图所示,若∠AOE和∠AOF是两个相邻的角,OM、ON分别是∠AOE和∠AOF的平分线,∠MON=90°,问:E、O、F三点在同一条直线上吗?若在,请说明理由.
如图所示,若∠AOE和∠AOF是两个相邻的角,OM、ON分别是∠AOE和∠AOF的平分线,∠MON=90°,问:E、O、F三点在同一条直线上吗?若在,请说明理由.考点:角平分线的定义
专题:
分析:根据角平分线的定义可知∠AOE=2∠AOM,∠AOF=2∠AON,由于∠MON=90°,可得到∠EOF=180°,从而求解.
解答:解:∵OM、ON分别是∠AOE和∠AOF的平分线,
∴∠AOE=2∠AOM,∠AOF=2∠AON,
∵∠MON=90°,
∴∠AOE+∠AOF=2∠AOM+2∠AON=2(∠AOM+∠AON)=2∠MON=180°,
∴E、O、F三点在同一条直线上.
∴∠AOE=2∠AOM,∠AOF=2∠AON,
∵∠MON=90°,
∴∠AOE+∠AOF=2∠AOM+2∠AON=2(∠AOM+∠AON)=2∠MON=180°,
∴E、O、F三点在同一条直线上.
点评:考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.关键是证明得到∠EOF=180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为了了解某校1000名七年级学生的体重情况,从中抽取了100名学生的体重,就这个问题,下面说法正确的是( )
| A、1000名学生的体重是总体 |
| B、1000名学生是总体 |
| C、每个学生是个体 |
| D、100名学生是所抽取的一个样本 |
 如图,反比例函数y1=
如图,反比例函数y1=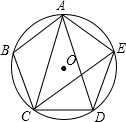 正五边形ABCDE内接于⊙O,连接AC,AD.
正五边形ABCDE内接于⊙O,连接AC,AD. 如图,点A的坐标为 (5,0),试在第一象限内网格的格点(网格线的交点)上找一点B,使其与点O、A构成等腰三角形,请写出图中所有满足条件的点B的坐标.
如图,点A的坐标为 (5,0),试在第一象限内网格的格点(网格线的交点)上找一点B,使其与点O、A构成等腰三角形,请写出图中所有满足条件的点B的坐标.