题目内容
6. 如图,AB=AC=2$\sqrt{3}$,∠A=30°,P为BC边上的一个动点,PD⊥AB、PE⊥AC,则PE+PD=$\sqrt{3}$.
如图,AB=AC=2$\sqrt{3}$,∠A=30°,P为BC边上的一个动点,PD⊥AB、PE⊥AC,则PE+PD=$\sqrt{3}$.
分析 连接AP、CF,然后求出△ABC的面积以及△ACP与△ABP的面积之和,化简后即可求出PE+PD
解答 解:连接AP,过点C作CF⊥AB于点F
∵∠A=30°,
∴CF=$\frac{1}{2}$AC=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$AB•CF=3
S△ACP+S△ABP=$\frac{1}{2}$AC•PF+$\frac{1}{2}$AB•PD=$\sqrt{3}$(PF+PD)
∵S△ABC=S△ACP+S△ABP
∴3=$\sqrt{3}$(PF+PD)
∴PF+PD=$\sqrt{3}$
点评 本题考查三角形的综合问题,解题的关键是根据含30度角的直角三角形的性质求出CF的高,然后利用三角形的面积关系求出PD+PF的值,本题属于基础题型.

练习册系列答案
相关题目
1.a,b,c为三个有理数,下列各式可写成a-b+c的是( )
| A. | a-(-b)-(+c) | B. | a-(+b)-(-c) | C. | a+(-b)+(-c) | D. | a+(-b)-(+c) |
18.画△ABC中BC边上的高,下面的画法中,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知mx2yn-1+4x2y9=0,(其中x≠0,y≠0)则m+n=( )
| A. | -6 | B. | 6 | C. | 5 | D. | 14 |
 如图,已知AB=AC,AD平分∠BAC,试说明∠EBD=∠ECD.
如图,已知AB=AC,AD平分∠BAC,试说明∠EBD=∠ECD.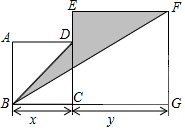 如图:四边形ABCD和四边形ECGF都是正方形,其边长分别为x、y(点B、C、G和点C、D、E分别在一条直线上)则图中阴影部分的面积为:$\frac{1}{2}{x}^{2}-\frac{1}{2}xy+\frac{1}{2}{y}^{2}$(用含x、y的代数式表示,且按x降幂排列)
如图:四边形ABCD和四边形ECGF都是正方形,其边长分别为x、y(点B、C、G和点C、D、E分别在一条直线上)则图中阴影部分的面积为:$\frac{1}{2}{x}^{2}-\frac{1}{2}xy+\frac{1}{2}{y}^{2}$(用含x、y的代数式表示,且按x降幂排列) 如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=$\frac{1}{3}$.
如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=$\frac{1}{3}$.