题目内容
 如图,在Rt△ABC中,AC=4,∠ACB=90°,∠B=30°.AD平分∠CAB交CB于D,点E是斜边AB上的一点,连接DE,当△ADE为直角三角形时,BE的长为
如图,在Rt△ABC中,AC=4,∠ACB=90°,∠B=30°.AD平分∠CAB交CB于D,点E是斜边AB上的一点,连接DE,当△ADE为直角三角形时,BE的长为考点:角平分线的性质,含30度角的直角三角形,勾股定理
专题:分类讨论
分析:求出∠CAD=30°,然后解直角三角形求出AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AB,再分①∠ADE=90°时,解直角三角形求出AE,然后根据BE=AB-AE计算即可得解;②∠AED=90°时,根据角平分线上的点到角的两边距离相等可得AE=AC,然后根据BE=AB-AE计算即可得解.
解答:解:∵∠ACB=90°,∠B=30°,AD平分∠CAB,
∴∠CAD=
(90°-30°)=30°,
∴AD=AC÷cos30°=4÷
=
,
∵∠B=30°,
∴AB=2AC=2×4=8,
①∠ADE=90°时,AE=AD÷cos30°=
÷
=
,
所以,BE=AB-AE=8-
=
;
②∠AED=90°时,
∵∠ACB=90°,AD平分∠CAB,
∴AE=AC=4,
∴BE=AB-AE=8-4=4,
综上所述,BE的长为
或4.
故答案为:
或4.
∴∠CAD=
| 1 |
| 2 |
∴AD=AC÷cos30°=4÷
| ||
| 2 |
8
| ||
| 3 |
∵∠B=30°,
∴AB=2AC=2×4=8,
①∠ADE=90°时,AE=AD÷cos30°=
8
| ||
| 3 |
| ||
| 2 |
| 16 |
| 3 |
所以,BE=AB-AE=8-
| 16 |
| 3 |
| 8 |
| 3 |
②∠AED=90°时,
∵∠ACB=90°,AD平分∠CAB,
∴AE=AC=4,
∴BE=AB-AE=8-4=4,
综上所述,BE的长为
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,解直角三角形,熟记各性质是解题的关键,难点在于分情况讨论.

练习册系列答案
相关题目
九年级某班一个合作学习小组共10名学生的体育加试成绩分别为:38,38,40,42,42,42,42,43,45,48,这组数据的众数和平均数分别是( )
| A、42,43 |
| B、38,42 |
| C、42,41 |
| D、42,42 |
定义新运算“*”:对于任意两个实数a、b,有a*b=b2-1,例如:6*4=42-1=15.那么当m为实数时,m*(m*
)=( )
| 2013 |
| A、20132-1 |
| B、20122-1 |
| C、20112-1 |
| D、m2-1 |
 如图,已知直线l:y=
如图,已知直线l:y=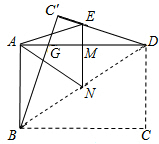 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为 小明骑自行车从家出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局沿一条道路步行回家,小明在邮局停留2分钟后沿原理以原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD、线段EF分别是表示
小明骑自行车从家出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局沿一条道路步行回家,小明在邮局停留2分钟后沿原理以原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD、线段EF分别是表示