题目内容
7.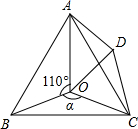 如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,
如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
分析 (1)根据全等三角形的性质得到OC=DC,根据等边三角形的判定定理证明即可;
(2)根据全等三角形的性质得到∠ADC=∠BOC=∠α=150°,结合图形计算即可;
(3)用反证法,假设△AOD能否为等边三角形,根据题意证明∠AOC+∠AOB+∠BOC不等于360°,推出矛盾;
(4)分∠AOD=∠ADO、∠AOD=∠OAD、∠ADO=∠OAD三种情况,根据等腰三角形的判定定理计算即可.
解答 (1)证明:∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形;
(2)△AOD是Rt△.
理由如下:
解:∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC-∠ODC=150°-60°=90°,
∴△AOD是Rt△;
(3)不能.理由:
解:由△BOC≌△ADC,得∠ADC=∠BOC=∠α.
若△AOD为等边三角形,
则∠ADO=60°,
又∵∠ODC=60°,
∴∠ADC=∠α=120°.
又∵∠AOD=∠DOC=60°,
∴∠AOC=120°,
又∵∠AOB=110°,
∴∠AOC+∠AOB+∠BOC=120°+120°+110°=350°<360°.
∴△AOD不可能为等边三角形;
(4)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-α-60°=190°-α,
∠ADO=∠ADC-∠ODC=α-60°,
∴∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°.
①当∠AOD=∠ADO时,190°-α=α-60°,∴α=125°.
②当∠AOD=∠OAD时,190°-α=50°,∴α=140°.
③当∠ADO=∠OAD时,α-60°=50°,∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
点评 本题考查的是全等三角形的判定和性质、等边三角形的判定、直角三角形的判定以及等腰三角形的判定,掌握相关的判定定理是解题的关键,注意分情况讨论思想的应用.

| A. | 3xy与xy2 | B. | -2a与a | C. | -3m与mn | D. | $\frac{1}{3}$a2b与b2a |
| A. | 6,8,12 | B. | 1,4,$\sqrt{3}$ | C. | 3,4,5 | D. | 2,2,$\sqrt{5}$ |
| 2015年10月18日起1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 上午8:20 | B站 | 次日12:20 |
| 2014年1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 下午14:30 | B站 | 第三日8:30 |
(1)请直接写出现在该次列车的运行时间是多少小时?
(2)现在该次列车的运行时间比以前缩短了多少小时?
(3)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果精确到个位)
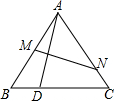 如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.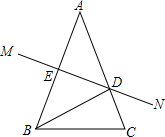 已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.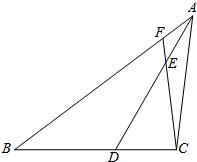 已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.
已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC. 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°