题目内容
19. 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°(1)求证:AC平分∠BAD;
(2)若AE=9,BE=3,求AD的长.
分析 (1)作CF⊥AD的延长线于F,再由条件就可以得出△CDF≌△CEB,就可以得出CF=CE,从而得出结论;
(2)先证△CFA≌△CEA,可以得出AF=AE,DF=BE,就可以求出DF的值从而得出结论.
解答 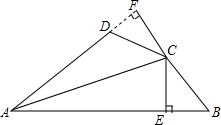 (1)证明:作CF⊥AD,交AD延长线与F
(1)证明:作CF⊥AD,交AD延长线与F
∵∠CDF+∠ADC=180°
∠ABC+∠ADC=180°
∴∠CDF=∠ABC,即∠EBC=∠CDF
∵CE⊥AB,那么∠CEB=∠CFD=90°
在△CFD和△CEB中,
$\left\{\begin{array}{l}{∠CEB=∠CFB}\\{∠EBC=∠CDF}\\{CD=CB}\end{array}\right.$,
∴△CDF≌△CBE(AAS)
∴CE=CF
∵CF⊥AD,CE⊥AB,CE=CF,
∴AC平分∠BAD;
(2)解:∵AC平分∠BAD
∴∠FAC=∠EAC
在△CFA和△CEA中,
$\left\{\begin{array}{l}{∠CEA=∠CFA}\\{∠FAC=∠EAC}\\{AC=AC}\end{array}\right.$,
∴△CFA≌△CEA(AAS),
∴AF=AE=9,
∵△CDF≌△CBE,
∴DF=BE=3,
∴AD=AF-FD=9-3=6.
点评 本题考查了全等三角形的判定与性质的运用,角平分线的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
4.如图在表中填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )


| A. | 74 | B. | 104 | C. | 126 | D. | 144 |
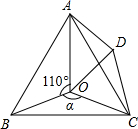 如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,
如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α, 如图,在△ABC中,∠ACB=3∠B,AB=10,AC=4,AD平分∠BAC,交BC于点D,CE⊥AD于E,则CE=3.
如图,在△ABC中,∠ACB=3∠B,AB=10,AC=4,AD平分∠BAC,交BC于点D,CE⊥AD于E,则CE=3. 从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.
从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.