题目内容
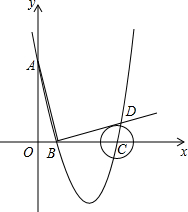如图，在平面直角坐标系中，顶点为（3，-4）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，5）．（1）求此抛物线的解析式；
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有什么位置关系，并给出证明；
（3）在抛物线对称轴上是否存在一点P，使△ACP是直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
考点：二次函数综合题
专题：
分析：（1）利用顶点式将点A的坐标代入即可求得a的值，从而确定二次函数的解析式；
（2）首先求得B（1，0），C（5，0），设切点为E，连接CE，根据Rt△ABO∽Rt△BCE得到比例式，从而求得CE=
；根据点C到对称轴x=3的距离为2，2＞
，从而确定抛物线的对称轴l与⊙C相离；
（3）分三个角可能为直角，利用直角三角形的性质求得点P的坐标即可．
（2）首先求得B（1，0），C（5，0），设切点为E，连接CE，根据Rt△ABO∽Rt△BCE得到比例式，从而求得CE=
| 4 | ||
|
| 4 | ||
|
（3）分三个角可能为直角，利用直角三角形的性质求得点P的坐标即可．
解答：（1）解：设抛物线解析式为：y=a（x-3）2-4，
将A（0，5）代入求得：a=1，
∴抛物线解析式为y=（x-3）2-4=x2-6x+5．
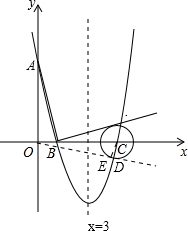
（2）抛物线的对称轴l与⊙C相离．
证明：令y=0，即x2-6x+5=0，得x=1或x=5，
∴B（1，0），C（5，0）．
如答图①所示，设切点为E，连接CE，由题意易证Rt△ABO∽Rt△BCE，
∴
=
，即
=
，
求得⊙C的半径CE=
；
而点C到对称轴x=3的距离为2，2＞
，
∴抛物线的对称轴l与⊙C相离．
（3）存在．
P1（3，-2），P2（3，8），P3（3，-1），P4（3，6）．
将A（0，5）代入求得：a=1，
∴抛物线解析式为y=（x-3）2-4=x2-6x+5．
（2）抛物线的对称轴l与⊙C相离．
证明：令y=0，即x2-6x+5=0，得x=1或x=5，
∴B（1，0），C（5，0）．
如答图①所示，设切点为E，连接CE，由题意易证Rt△ABO∽Rt△BCE，
∴
| AB |
| BC |
| OB |
| CE |
| ||
| 4 |
| 1 |
| CE |
求得⊙C的半径CE=
| 4 | ||
|
而点C到对称轴x=3的距离为2，2＞
| 4 | ||
|
∴抛物线的对称轴l与⊙C相离．
（3）存在．
P1（3，-2），P2（3，8），P3（3，-1），P4（3，6）．
点评：本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和直角三角形的性质．在求有关动点问题时要注意分析题意分情况讨论结果．
练习册系列答案
相关题目
将抛物线y=x2-4x+5的顶点A向左平移2个单位长度得到点A′，则点A′的坐标是（ ）
| A、（2，3） |
| B、（2，-1） |
| C、（4，1） |
| D、（0，1） |