题目内容
端午节即将到来,武汉端午食品开始热销.近日,武汉各大超市相关商品纷纷打折促销,带动销量同比上涨30%.某名牌20枚盒装的皮咸蛋成本为20元∕盒投放市场进行试销.经过调查,得到如下数据:
(1)上表中x、y的各组对应值满足我们学习过的三种函数(即一次函数、反比例函数和二次函数)关系中的一种,试求y与x的函数关系式,不要求写出自变量的取值范围;
(2)当销售单价定为多少时,超市试销该皮咸蛋每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)市物价部门规定,20枚盒装的皮咸蛋销售单价最高不能超过45元/盒,那么销售单价定为多少时,超市试销该皮咸蛋每天获得的利润最大?
| 销售单价 (元∕盒) | … | 25 | 35 | 45 | … |
| 每天销售量 (盒) | … | 550 | 450 | 350 | … |
(2)当销售单价定为多少时,超市试销该皮咸蛋每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)市物价部门规定,20枚盒装的皮咸蛋销售单价最高不能超过45元/盒,那么销售单价定为多少时,超市试销该皮咸蛋每天获得的利润最大?
考点:二次函数的应用
专题:
分析:(1)根据题意利用待定系数法求一次函数解析式即可;
(2)根据利润=销量×每件利润,进而利用配方法求出二次函数最值即可;
(3)利用二次函数增减性进而得出答案.
(2)根据利润=销量×每件利润,进而利用配方法求出二次函数最值即可;
(3)利用二次函数增减性进而得出答案.
解答:解:(1)由表中数据判断,销售量y与x之间的函数关系不是反比例函数关系.
假设是一次函数关系,可设函数解析式为y=kx+b.则
解得:
,
将x=45,y=350,代入检验,满足条件.
故其解析式为y=-10x+800;
(2)设超市试销该皮咸蛋每天获得的利润是W元,依题意得
W=(x-20)(-10x+800)=-10x2+1000x-16000=-10(x-50)2+9000,
∴当x=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,超市试销该皮咸蛋每天获得的利润最大,最大利润是9000元.
(3)对于函数 W=-10(x-50)2+9000,
∵a=-10<0,当x≤45时,
∴W的值随着x值的增大而增大,
∴销售单价定为45元/盒时,超市试销该皮咸蛋每天获得的利润最大.
假设是一次函数关系,可设函数解析式为y=kx+b.则
|
解得:
|
将x=45,y=350,代入检验,满足条件.
故其解析式为y=-10x+800;
(2)设超市试销该皮咸蛋每天获得的利润是W元,依题意得
W=(x-20)(-10x+800)=-10x2+1000x-16000=-10(x-50)2+9000,
∴当x=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,超市试销该皮咸蛋每天获得的利润最大,最大利润是9000元.
(3)对于函数 W=-10(x-50)2+9000,
∵a=-10<0,当x≤45时,
∴W的值随着x值的增大而增大,
∴销售单价定为45元/盒时,超市试销该皮咸蛋每天获得的利润最大.
点评:此题主要考查了二次函数的应用以及待定系数法求一次函数解析式和二次函数增减性应用,利用二次函数增减性得出最值是解题关键.

练习册系列答案
相关题目
多项式4x2-7x+5-2+6x中的同类项有( )
| A、7x和6x |
| B、5和-2 |
| C、-7x和6x,5和-2 |
| D、7x和6x,5和2 |
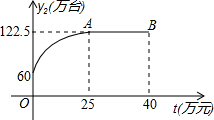 某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=3x+25,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=3x+25,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.
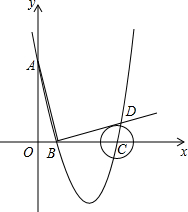 如图,在平面直角坐标系中,顶点为(3,-4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(3,-4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,5).