题目内容
半径为10cm的圆内接正三角形的边长为 .
考点:正多边形和圆
专题:
分析:欲求△ABC的边长,把△ABC中BC边当弦,作BC的垂线,在Rt△BOD中,求BD的长;根据垂径定理知:BC=2BD,从而求正三角形的边长.
解答: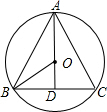 解:如图所示:
解:如图所示:
∵半径为10cm的圆的内接正三角形,
∴在Rt△BOD中,OB=10cm,∠OBD=30°,
∴BD=cos30°×OB=
×10=5
(cm),
∵BD=CD,
∴BC=2BD=10
cm.
故它的内接正三角形的边长为10
cm.
故答案为10
cm.
 解:如图所示:
解:如图所示:∵半径为10cm的圆的内接正三角形,
∴在Rt△BOD中,OB=10cm,∠OBD=30°,
∴BD=cos30°×OB=
| ||
| 2 |
| 3 |
∵BD=CD,
∴BC=2BD=10
| 3 |
故它的内接正三角形的边长为10
| 3 |
故答案为10
| 3 |
点评:本题主要考查了正多边形和圆,根据正三角形的性质得出,∠OBD=30°是解题关键,此题难度一般,是一道比较不错的试题.

练习册系列答案
相关题目
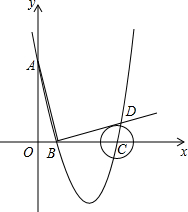 如图,在平面直角坐标系中,顶点为(3,-4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(3,-4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,5). 已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且
已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则