题目内容
1.(1)先化简,再求值:$\frac{{x}^{2}}{x-1}$÷(1+$\frac{1}{{x}^{2}-1}$),其中x=2017.(2)已知方程x2-2x+m-3=0有两个相等的实数根,求m的值.
分析 (1)根据分式的除法和加法可以化简题目中的式子,然后将x的值代入即可解答本题;
(2)根据方程x2-2x+m-3=0有两个相等的实数根,可知△=0,从而可以求得m的值.
解答 解:(1)$\frac{{x}^{2}}{x-1}$÷(1+$\frac{1}{{x}^{2}-1}$)
=$\frac{{x}^{2}}{x-1}÷\frac{{x}^{2}-1+1}{{x}^{2}-1}$
=$\frac{{x}^{2}}{x-1}•\frac{(x+1)(x-1)}{{x}^{2}}$
=x+1,
当x=2017时,原式=2017+1=2018;
(2)∵方程x2-2x+m-3=0有两个相等的实数根,
∴△=(-2)2-4×1×(m-3)=0,
解得,m=4.
点评 本题考查根的判别式、分式的化简求值,解答本题的关键是明确分式化简求值的方法和一元二次方程有两个相等的实数根时△=0.

练习册系列答案
相关题目
6.实数2+a是无理数,则a的值一定不是( )
| A. | 2$\sqrt{2}$ | B. | -2 | C. | $\sqrt{2}$ | D. | $\root{3}{2}$ |
11.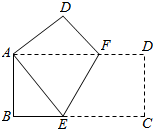 如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )
如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )
 如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )
如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )| A. | 3cm | B. | 4cm | C. | 2cm | D. | 5cm |
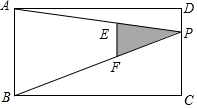 一只小狗在如图所示的矩形草地ABCD内自由的玩耍,点P是矩形的边CD上一点,点E、点F分别为PA,PB的中点,连接EF,则这只小狗跑到△PEF内的概率是$\frac{1}{8}$.
一只小狗在如图所示的矩形草地ABCD内自由的玩耍,点P是矩形的边CD上一点,点E、点F分别为PA,PB的中点,连接EF,则这只小狗跑到△PEF内的概率是$\frac{1}{8}$.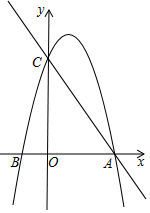 如图,直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).
如图,直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).