题目内容
14.已知:顺次连接矩形各边的中点,得到一个菱形,如图1;再次顺次连接菱形各边的中点,得到一个新的矩形,如图2;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图3;如此反复操作下去,则第2 013个图形中直角三角形的个数有( )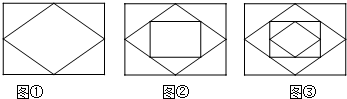
| A. | 4 028个 | B. | 4 024个 | C. | 4 022个 | D. | 2 012个 |
分析 观察图形可知,两个图形为一个组,直角三角形的个数相同,且都是4的倍数,然后求出第2013个图形的组数,计算即可得解.
解答 解:图①图②的直角三角形的个数相同,都是4,4=4×1,
图③图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013图2014的直角三角形的个数相同,都是4×$\frac{2014}{2}$=4028.
故选:A.
点评 此题考查图形的变化规律,观察图形,得到变化规律:连续两个图形的直角三角形的个数相同是解题的关键.

练习册系列答案
相关题目
19.下面是几个城市某年一月份的平均温度,其中平均温度最低的城市是( )
| A. | 利川4.2℃ | B. | 广州13.5℃ | C. | 北京-4.8℃ | D. | 兰州-3.4℃ |
3.甲、乙两人在相同的条件下各射靶10次,他们命中的环数的平均数相等,但方差不同,其中S甲2=1.2,S乙2=3,那么射击成绩较稳定的是( )
| A. | 甲 | B. | 乙 | C. | 甲、乙相同 | D. | 不能确定 |

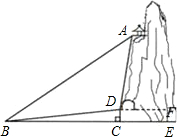 某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.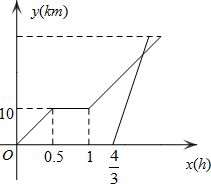 周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后达到甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同的路线前往乙地,他们离家的路程y(km)与小明离家时间x(h)之间的关系如图所示,已知妈妈驾车的速度是小明汽车速度的3倍
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后达到甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同的路线前往乙地,他们离家的路程y(km)与小明离家时间x(h)之间的关系如图所示,已知妈妈驾车的速度是小明汽车速度的3倍