题目内容
1.已知关于x、y的方程组$\left\{\begin{array}{l}{2x+3y=3m+7}\\{x-y=4m+1}\end{array}\right.$的解是一对正数.(1)试用m表示方程组的解;
(2)求m的取值范围;
(3)化简:$\sqrt{(m-1)^{2}}$+|m+$\frac{2}{3}$|.
分析 (1)把m看做已知数,表示出方程组的解即可;
(2)根据x与y为正数列出不等式组,求出不等式组的解集即可确定出m的范围;
(3)由m的范围确定出m-1与m+$\frac{2}{3}$的正负,利用二次根式的性质及绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)$\left\{\begin{array}{l}{2x+3y=3m+7①}\\{x-y=4m+1②}\end{array}\right.$,
①+②×3得:5x=15m+10,即x=3m+2,
把x=3m+2代入②得:y=-m+1,
则方程组的解为$\left\{\begin{array}{l}{x=3m+2}\\{y=-m+1}\end{array}\right.$;
(2)由题意得:$\left\{\begin{array}{l}{3m+2>0}\\{-m+1>0}\end{array}\right.$,
解得:-$\frac{2}{3}$<m<1;
(3)∵-$\frac{2}{3}$<m<1,
∴m-1<0,m+$\frac{2}{3}$>0,
则原式=1-m+m+$\frac{2}{3}$=$\frac{5}{3}$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.二次函数y=(x-1)2+3的最小值是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
 平面直角坐标系中,A(-2,0),B(-3,4),试在y轴上求作一点C,使AC+BC最短,求出点C的坐标.
平面直角坐标系中,A(-2,0),B(-3,4),试在y轴上求作一点C,使AC+BC最短,求出点C的坐标.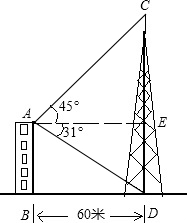 如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖C的仰角是45°,而塔底部D的俯角是31°,求佛山电视塔CD的高度.(tan31°=0.600,结果精确到1米)
如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖C的仰角是45°,而塔底部D的俯角是31°,求佛山电视塔CD的高度.(tan31°=0.600,结果精确到1米) 如图,AB∥DE,探究∠B、∠C、∠D、∠F的关系.
如图,AB∥DE,探究∠B、∠C、∠D、∠F的关系.