题目内容
8.若实数m,n满足(m-1)2+$\sqrt{n+2}$=0,则(m+n)5=-1.分析 根据非负数的性质可求出m、n的值,进而可求出(m+n)5的值.
解答 解:由题意知,
m,n满足(m-1)2+$\sqrt{n+2}$=0,
∴m=1,n=-2,
∴(m+n)5=(1-2)5=-1.
故答案为:-1.
点评 此题主要考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
19.下列实数是无理数的是( )
| A. | 5 | B. | 0 | C. | $\frac{1}{3}$ | D. | $\sqrt{2}$ |
16.对于任意的正数m、n定义运算※为:m※n=$\left\{\begin{array}{l}{\sqrt{m}-\sqrt{n}(m≥n)}\\{\sqrt{m}+\sqrt{n}(m<n)}\end{array}\right.$,计算(3※2)×(8※12)的结果为( )
| A. | 2-4$\sqrt{6}$ | B. | 2 | C. | 2$\sqrt{5}$ | D. | 20 |
13.甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )
| A. | $\frac{120}{x}$=$\frac{100}{x-4}$ | B. | $\frac{120}{x}$=$\frac{100}{x+4}$ | C. | $\frac{120}{x-4}$=$\frac{100}{x}$ | D. | $\frac{120}{x+4}$=$\frac{100}{x}$ |
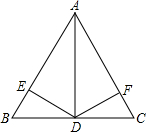 如图,AD平分∠BAC,DE⊥AB,DF⊥AC,试说明△ADE≌△ADF.
如图,AD平分∠BAC,DE⊥AB,DF⊥AC,试说明△ADE≌△ADF.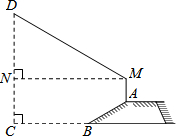 如图,防洪大坝的横断面是梯形,背水面AB的坡比i=1:$\sqrt{3}$(指坡面的铅直高度与水平宽度的比),且AB=18m.身高为1.8m的小彬站在大堤A点,测得高压电线杆顶端点D的仰角为30°.已知地面CB的宽为28m,求高压电线杆CD的高度.
如图,防洪大坝的横断面是梯形,背水面AB的坡比i=1:$\sqrt{3}$(指坡面的铅直高度与水平宽度的比),且AB=18m.身高为1.8m的小彬站在大堤A点,测得高压电线杆顶端点D的仰角为30°.已知地面CB的宽为28m,求高压电线杆CD的高度.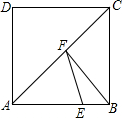 如图,在边长为4的长方形ABCD中,E是AB边上一点,且AE=3,点F为对角线AC上的动点,则△BEF周长的最小值为( )
如图,在边长为4的长方形ABCD中,E是AB边上一点,且AE=3,点F为对角线AC上的动点,则△BEF周长的最小值为( ) 如图,由A到B的方向是东偏南30°.
如图,由A到B的方向是东偏南30°.